- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Electrical & Electronic Engineering Journal
(Discontinued)
ISSN: 1874-1290 ― Volume 13, 2019
A Novel Positioning Algorithm Based on Self-adaptive Algorithm of RBF Network
Jin Ren*, Jingxing Chen, Liang Feng
Abstract
Much attention has been paid to Taylor series expansion (TSE) method these years, which has been extensively used for solving nonlinear equations for its good robustness and accuracy of positioning. A Taylor-series expansion location algorithm based on the RBF neural network (RBF-TSE) is proposed before to the performance of TSE highly depends on the initial estimation. In order to have more accurate and lower cost,a new Taylor-series expansion location algorithm based on Self-adaptive RBF neural network (SA-RBF-TSE) is proposed to estimate the initial value. The proposed algorithm is analysed and simulated with several other algorithms in this paper.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 141
Last Page: 148
Publisher Id: TOEEJ-10-141
DOI: 10.2174/1874129001610010141
Article History:
Received Date: 19/02/2016Revision Received Date: 14/07/2016
Acceptance Date: 22/07/2016
Electronic publication date: 21/11/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the School of Electronic and Information Engineering, North China University of Technology, No.5 Jinyuanzhuang Road, Beijing, P.R. China; Tel: 86 +13522323925; Fax: 86 +010-88803130; E-mail: rj@ncut.edu.cn
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 19-02-2016 |
Original Manuscript | A Novel Positioning Algorithm Based on Self-adaptive Algorithm of RBF Network | |
1. INTRODUCTION
With the rapid development of mobile communication technology, mobile positioning technology has become the hot research topic. There have been different positioning systems, such as angle-of-arrival (AOA), time-of-arrival (TOA), time-difference-of-arrival (TDOA), assisted GPS (A-GPS) and Fingerprint [1L.M. Winternitz, W.A. Bamford, and G.W. Heckler, "A GPS receiver for high-altitude satellite navigation", IEEE J. Sel. Top. Signal Process., vol. 3, no. 4, pp. 541-556, 2009.
[http://dx.doi.org/10.1109/JSTSP.2009.2023352] ]. Among them, TDOA method requires fewer equipment changes and does not need a mobile station (MS) and strict time synchronization between the base stations (BS), thus given immense attention. Taylor series expansion algorithm (TSE), Chan algorithm (Chan),least squares algorithm (LS). Least square and Taylor series algorithm (LS-TSE) is based on the TDOA location algorithm. The derivation process of the Chan algorithm is based on TDOA error smaller, the premise is the ideal of zero mean gaussian random variables, so for the NLOS error is bigger in the environment of TDOA measurements, it will have great influence on the performance of the algorithm. As LS algorithm does not need to consider the statistical properties of the error, in the NLOS environment, position precision is slightly better than Chan algorithm. Taylor series expansion method [2M. Soltanian, A.M. Pezeshk, and A. Mahdavi, "A new iterative position finding algorithm based on Taylor series expansion", In: Proceedings of 2011 19th Iranian Conference on Electrical Engineering(ICEE), Maryam, Dallali, 2011, pp. 1-4., 3X. J. Yu, and W. Wei, "A new TDOA location technique based on Taylor series expansion in cellular networks", In: Proceedings of the 4th International Conference on Parallel and Distributed Computing, Applications and Technologie, Chengdu, China, 2003, pp. 378-381.] needs an early and close to the actual location of estimated position to guarantee the constringency of the algorithm, positioning accuracy is higher than that in the NLOS environment Chan algorithm and LS algorithm. But Taylor algorithm in NLOS environment positioning accuracy of positioning accuracy is far lower than LOS environment. So, how to reduce the TDOA measurements of NLOS error is important for Taylor algorithm applying in the NLOS environment. RBF network is typical of the forward neural network with functions of nonlinear continuum approximation. TDOA location algorithm is based on RBF neural network [4T. G. Hua, D. Jing, and N. C. Jian, "Series type of neural network and its application and research in forecasting of river floods", Res. Water Resources., vol. 24, no. 2, pp. 4-5, 2003., 5C.X. Yun, M. Qiang, and T. Alkharobi, "New neural networks based on Taylor series and their research", In: Proceedings of 2nd IEEE International Conference on Computer Science and Information Technology., Beijing, China, 2009, pp. 291-194.]. Through the comprehensive utilization of multiple base station TDOA measurements, the NLOS error correction, the TDOA measurements near LOS the measured value of the environment, reusing Taylor algorithm is used to estimate position, make it has higher positioning accuracy in NLOS environment.
This paper proposed a Self-adaptive algorithm of RBF network (SA-RBF-TSE) [6W.L biao, and F Jian, "Study of self-adaptive RBF neural network control method for the engine idle speed control", In: Proceedings of 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet)., XianNing, China, 2011, pp. 2633-2636., 7K. Meng, Z.Y. Dong, D.H. Wang, and K.P. Wong, "A self-adaptive RBF neural network classifier for transformer fault analysis", IEEE Trans. Power Syst., vol. 25, no. 3, pp. 1350-1360, 2010.
[http://dx.doi.org/10.1109/TPWRS.2010.2040491] ] to correct TDOA measurements. The algorithm does not need to make sure the number of RBF and center vector firstly. In the process, according to the distribution of the errors in the input space, the number of RBF adaptively increasesand adjusts the center vector appropriately. Based on the corresponding deletion policy to make the number of RBF, the policy is the comprehensive evaluation of RBF network contribution firstly, and then deleting the small contributions to RBF, for the network structure always keeps it simple.
2. TDOA MEASUREMENTS CORRECTION BASED ON RBF NEURAL NETWORK
RBF network is a kind of three-layer feedforward network [8P. Singh, and S. Agrawal, "TDOA based node localization in WSN using neural networks", In: Proceedings of 2013 International Conference on Communication Systems and Network Technologies (CSNT), Gwalior, India, 2013, pp. 400-404.
[http://dx.doi.org/10.1109/CSNT.2013.90] ], composed of the input layer and output layer and hidden layer. Among them, input layers and output layers are composed of linear neurons; Hidden layer activation function (kernel functions) using center attenuation of radial symmetric nonnegative nonlinear function, its function is to input signal in response to local produce. Weights between the input layer and hidden layer are fixed to 1, and only the weights between the hidden layer and output layer are adjustable.
Input layer by seven related base station is provided by the six TDOA measurements. The input vector is: x = [x1, x2, x3, x4, x5, x6]T = [TDOA21, TDOA31, TDOA41, TDOA51, TDOA61]T. The role of hidden layer nodes function of the input signal in the local response, when the central range near the basis function of the input signal, the output of hidden layer nodes will produce larger, so the network has good local approximation ability. The choice of basis function is a Gaussian function:
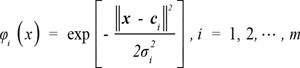 |
(1) |
where x is the input vector; ci is the centre of the ith a basis function, and the same dimension vector of x; M determines the width of the basis function around a central point; m is the number of unit perception. 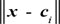 is a vector norm of x - ci. φi(x) is only a maximum value in the ci and φi(x) retuces quickly to zero with the increase of
is a vector norm of x - ci. φi(x) is only a maximum value in the ci and φi(x) retuces quickly to zero with the increase of 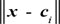 . Output layer consists of six neurons, the output of the adjusted TDOA value. The output vector is:
. Output layer consists of six neurons, the output of the adjusted TDOA value. The output vector is:
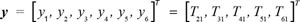 |
(2) |
3. TDOA MEASUREMENTS CORRECTION BASED ON PROPOSED ALGORITHM
The algorithm proposed in this paper is according to the network output error in the non-uniform distribution of the input space. Through adding and deleting network parameters on adjustment strategy adaptively, changes the size of RBF network and makes network an approximation and generalization ability to achieve high-performance requirements.
Self-Adaptive RBF neural network algorithm (SA-RBF-TSE) [6W.L biao, and F Jian, "Study of self-adaptive RBF neural network control method for the engine idle speed control", In: Proceedings of 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet)., XianNing, China, 2011, pp. 2633-2636., 7K. Meng, Z.Y. Dong, D.H. Wang, and K.P. Wong, "A self-adaptive RBF neural network classifier for transformer fault analysis", IEEE Trans. Power Syst., vol. 25, no. 3, pp. 1350-1360, 2010.
[http://dx.doi.org/10.1109/TPWRS.2010.2040491] ] of the specific process is as shown in Fig. (1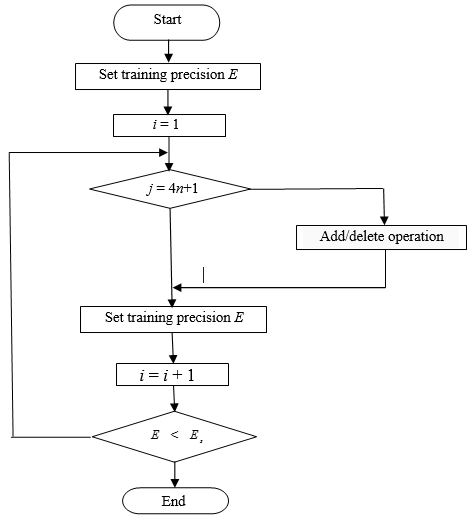 ). Before RBF training determines permissible error Es, as a condition of the end of the training. The whole process, in general, can be divided into three parts of the algorithm. The first part is the centre of the hidden layer nodes and the weights between the hidden layer and output layer. In this paper, using the gradient descent method, each cycles time, adjust accordingly. The second part is to perform to add operation. Add the strategy is based on the output error in the input space distribution inhomogeneity and proposed. If you execute the operation frequency, not only can reduce the centre of the hidden layer nodes and weights to adjust speed, and can cause an excessive number of hidden layer nodes, increase the amount of calculation and lead to excessive fitting. Considering the above factors, adopt the way of intermittent performing added operation, only when i = 4n+1 (n = 0, 1, 2,), add operation to perform. The third part is the deletion operation. If you execute the operation frequency, for some of the new increase of the hidden layer nodes, the centre position and weight may be able to adjust the deleted nodes, so also with the method of batch execution. When i = 8m + 7 (m = 0, 1, 2,), execute the delete operation.
). Before RBF training determines permissible error Es, as a condition of the end of the training. The whole process, in general, can be divided into three parts of the algorithm. The first part is the centre of the hidden layer nodes and the weights between the hidden layer and output layer. In this paper, using the gradient descent method, each cycles time, adjust accordingly. The second part is to perform to add operation. Add the strategy is based on the output error in the input space distribution inhomogeneity and proposed. If you execute the operation frequency, not only can reduce the centre of the hidden layer nodes and weights to adjust speed, and can cause an excessive number of hidden layer nodes, increase the amount of calculation and lead to excessive fitting. Considering the above factors, adopt the way of intermittent performing added operation, only when i = 4n+1 (n = 0, 1, 2,), add operation to perform. The third part is the deletion operation. If you execute the operation frequency, for some of the new increase of the hidden layer nodes, the centre position and weight may be able to adjust the deleted nodes, so also with the method of batch execution. When i = 8m + 7 (m = 0, 1, 2,), execute the delete operation.
3.2. Addition Strategy
Add strategy considering the network output error in the input space of non-uniform distribution. Need statistics each input vector to produce the output of the error, and then by comparing the find out the pointing error is relatively large, again in the near properly inserted into the hidden layer nodes.
Set (xk, yk), k = 1, 2,..., N is a set of training samples, the initial time, the number of hidden layer nodes is zero, each adding operation, according to the following guidelines determine whether add the hidden layer nodes:
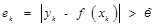 |
(3) |
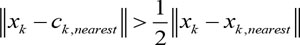 |
(4) |
where
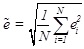 is the mean square error (MSE) of network output;
is the mean square error (MSE) of network output;
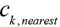 and
and
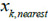 are respectively correspond to the input vector xk closest to the center of hidden layer nodes and the input vector. If you meet the adding conditions, will be (xk + xk,nearest)/2 is set to the new center of hidden layer nodes, ek set as the new node weights,
are respectively correspond to the input vector xk closest to the center of hidden layer nodes and the input vector. If you meet the adding conditions, will be (xk + xk,nearest)/2 is set to the new center of hidden layer nodes, ek set as the new node weights,
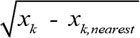 set as center width.
set as center width.
3.3. Deletion Operation
Due to the RBF neural network is one kind of local awareness network, the total output of network depends on the weights between the hidden layer and output layer and hidden layer nodes center and the distance between the input vectors. In training, the selection of training samples is relatively sparse. When one hidden layer node center is far away from each input vector, even if its weight is a larger number, also won't have much of an impact on output. At the end of the training in the process of inspection, inspection data are generally more dense, if some input vector is close to the hidden layer centre, the output will be a big impact, this makes the network generalization ability becomes poor. Therefore need to develop a strategy to remove the hidden layer nodes, the deletion policy is introduced.
The deletion policy is for each hidden layer nodes of the network put forward with the contribution of different sizes. The greater contribution of nodes will be kept; smaller contribution of nodes will be deleted. For any hidden layer nodes i, use the ϕ to show its contribution to the whole network.
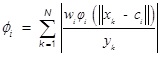 |
(5) |
Before delete execution operation to the normalized processing of ϕi, like
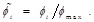 The final judgment rule is: if,
The final judgment rule is: if,
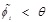 the ith hidden layer nodes are removed, including θ for decision threshold.
the ith hidden layer nodes are removed, including θ for decision threshold.
The gradient descent method is used to adjust the centre of the hidden layer nodes and weights in the process, need to compute each input vector of the corresponding output error ek, and the output value of each hidden layer nodes .
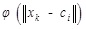 And also need to compute ek and
And also need to compute ek and
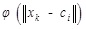 when perform add and remove operations. In order to reduce the amount of calculation and improve operation efficiency, can adjust the right of the centre of the hidden layer and the value in the process of saving ek and
when perform add and remove operations. In order to reduce the amount of calculation and improve operation efficiency, can adjust the right of the centre of the hidden layer and the value in the process of saving ek and
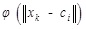 .
.
3.4. RBF Network Parameter Adjustment
In this paper, the gradient descent method is used to adjust the RBF centre position and the weights of hidden layer nodes. Set the number of hidden layer nodes for m, a total of N groups training sample: (x, y) = {(x1, y1), (x2, y2), ..., (xN, yN)}.The actual output of neural network:
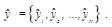 Selection of the mean square error as the error function, take μ1 and μ2 for vector.
Selection of the mean square error as the error function, take μ1 and μ2 for vector.
(1) Adjust the weights of hidden layer nodes
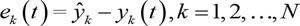 |
(6) |
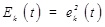 |
(7) |
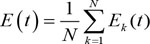 |
(8) |
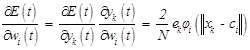 |
(9) |
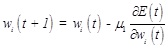 |
(10) |
(2) Adjust the center of the hidden layer nodes
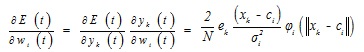 |
(11) |
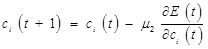 |
(12) |
4. TAYLOR SERIES EXPANSION LOCALIZATION ALGORITHM
First use trained RBF network to simulate TDOA measurements, then Taylor algorithm [9Y. Kegen, Y.J. Guo, and I. Oppermann, "Modified taylor series expansion based positioning algorithms", In: Proceedings of IEEE Vehicular Technology Conference, Singapore, 2008, pp. 2656-2660.] is adopted to improve the position estimation using the revised TDOA value. Set MS coordinates to (x, y), participate in the positioning of BSi coordinates to (xi, yi), the number is M, BS1 is the service station, c is the wave propagation speed, according to the measured wave propagation time (TOA) to establish the following distance equation:
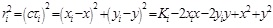 |
(13) |
where Ki = x2i + y2i
Let ri, 1 be the distance between the BSi and BS1:
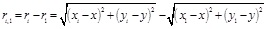 |
(14) |
Equation (14) in selected MS initial position makes Taylor expansion, ignore the second order more weight, Equation (14) will be got:
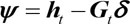 |
(15) |
where,
 |
where ri,
 is the initial position and the distance between the base station. Weighted least-square solution is in Equation (16):
is the initial position and the distance between the base station. Weighted least-square solution is in Equation (16):
 |
(16) |
where Q is the covariance matrix of TDOA measurements, ri,
 can be computed with
can be computed with
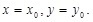 In the next recursive,
In the next recursive,
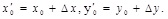 Repeat the process until the Δx, Δy is small enough to satisfy a set threshold:
Repeat the process until the Δx, Δy is small enough to satisfy a set threshold:
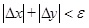 . At this time,
. At this time,
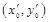 is the estimate position (x, y) of MS.
is the estimate position (x, y) of MS.
5. SIMULATION
Assume that the 7 base station coordinates are (0,0),
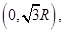
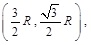
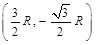
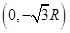
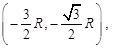
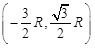 , respectively, where R is the cell radius, value is 2000m. The simulation of distance measurement di = Ri + Rinoise + Rinlos, where Rinoise is measurement error, can be thought of as zero mean Gaussian variables and the variance
, respectively, where R is the cell radius, value is 2000m. The simulation of distance measurement di = Ri + Rinoise + Rinlos, where Rinoise is measurement error, can be thought of as zero mean Gaussian variables and the variance 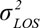 of in general, assuming that the standard deviation of 10 m here; R inlos is NLOS error and the variance of
of in general, assuming that the standard deviation of 10 m here; R inlos is NLOS error and the variance of 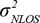 Gaussian distribution, unable to carry on the accurate modeling, so that it is evenly distributed between 0 and MAX random variables, including MAX to determine a value [10C.Y. Tong, T.W. Yue, S.H. Cheung, and C.P. Chung, "Time-of-arrival based localization under NLOS conditions", IEEE Transactions Vehicular Technology, vol. 55, no. 1, pp. 17-24, 2006.
Gaussian distribution, unable to carry on the accurate modeling, so that it is evenly distributed between 0 and MAX random variables, including MAX to determine a value [10C.Y. Tong, T.W. Yue, S.H. Cheung, and C.P. Chung, "Time-of-arrival based localization under NLOS conditions", IEEE Transactions Vehicular Technology, vol. 55, no. 1, pp. 17-24, 2006.
[http://dx.doi.org/10.1109/TVT.2005.861207] ].
Under the condition of LOS, Rinlos is zero, which shows measuring distance is the sum of the actual distance and the measurement noise. In NLOS condition, R inlos is not zero and is the dominant position, and measuring distance mainly inclusion of the actual distance and NLOS error.
In this paper, the proposed Taylor-series expansion location algorithm based on Self-adaptive RBF neural network (SA-RBF-TSE) algorithm is compared with Chan algorithm (Chan), LS algorithm (LS), Taylor series expansion algorithm (TSE), Least square and Taylor series algorithm (LS-TSE) and Taylor-series expansion location algorithm based on the RBF neural network (RBF-TSE), performance results areobtained by N times Monte Carlo simulation, and adopt the following root mean square error (RMSE) aspositioning error evaluation indexes:
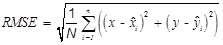 |
(17) |
where (x,y) is the true location of the unknown node,
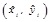 is the ith experimental estimate of the unknown node position, and n is simulation times.
is the ith experimental estimate of the unknown node position, and n is simulation times.
Fig. (2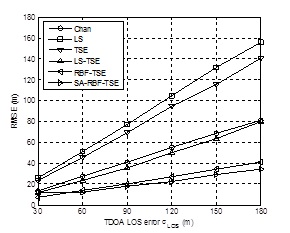 ) shows the relationship between Measurement noise standard deviation σ LOS and RMSE. With the increase of σ LOS, an error of all position the algorithm increases, compared with Chan, LS, TSE, LS-TSE and RBF-TSE, the positioning precision of SA-RBF-TSE on average increased by 55.26%, 76.57%, 73.80%, 51.60% and 10.81% respectively. Fig. (3
) shows the relationship between Measurement noise standard deviation σ LOS and RMSE. With the increase of σ LOS, an error of all position the algorithm increases, compared with Chan, LS, TSE, LS-TSE and RBF-TSE, the positioning precision of SA-RBF-TSE on average increased by 55.26%, 76.57%, 73.80%, 51.60% and 10.81% respectively. Fig. (3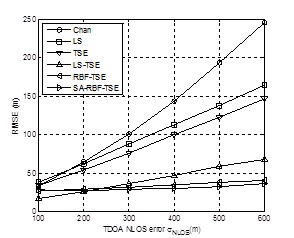 ) is RMSE performances of positioning Algorithms based on the NLOS error σ NLOS effect. Fig. (3
) is RMSE performances of positioning Algorithms based on the NLOS error σ NLOS effect. Fig. (3 ) shows, with the increase of NLOS error σ NLOS , a sharp rise in the positioning error of Chan, LS and TSE. SA-RBF-TSE under the influence of NLOS error σ NLOS is minimal and has the highest positioning accuracy than other algorithms. When the number of NLOS error σ NLOS is 500m, SA-RBF-TSE positioning accuracy compared with Chan, LS, TSE, LS-TSE and RBF-TSE is increased by 83.41%, 76.74%, 73.80%, 45.08% and 15.14% respectively.
) shows, with the increase of NLOS error σ NLOS , a sharp rise in the positioning error of Chan, LS and TSE. SA-RBF-TSE under the influence of NLOS error σ NLOS is minimal and has the highest positioning accuracy than other algorithms. When the number of NLOS error σ NLOS is 500m, SA-RBF-TSE positioning accuracy compared with Chan, LS, TSE, LS-TSE and RBF-TSE is increased by 83.41%, 76.74%, 73.80%, 45.08% and 15.14% respectively.
 |
Fig. (2) RMSE performance comparison of positioning Algorithms on Measurement noise standard deviation σ LOS. |
 |
Fig. (3) RMSE performance comparison of positioning Algorithms on NLOS error σ NLOS. |
Fig. (4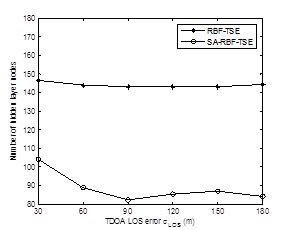 ) shows the number of hidden layer nodes for RBF-TSE and SA-RBF-TSE on different Measurement noise standard deviation σ LOS . Fig. (5
) shows the number of hidden layer nodes for RBF-TSE and SA-RBF-TSE on different Measurement noise standard deviation σ LOS . Fig. (5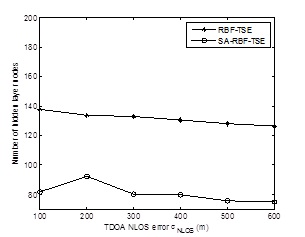 ) shows the number of hidden layer nodes for RBF-TSE and SA-RBF-TSE on different NLOS error σ NLOS under Measurement noise standard deviation σ LOS is 30m. From Figs. (4
) shows the number of hidden layer nodes for RBF-TSE and SA-RBF-TSE on different NLOS error σ NLOS under Measurement noise standard deviation σ LOS is 30m. From Figs. (4 and 5
and 5 ), the RBF training determines permissible error threshold needed for the number of hidden layer nodes,SA-RBF-TSE is less than RBF-TSE obviously. Therefore, nodes loss of SA-RBF-TSE is better than RBF-TSE under the condition of LOS/NLOS.
), the RBF training determines permissible error threshold needed for the number of hidden layer nodes,SA-RBF-TSE is less than RBF-TSE obviously. Therefore, nodes loss of SA-RBF-TSE is better than RBF-TSE under the condition of LOS/NLOS.
 |
Fig. (4) Number of hidden layer nodes for RBF-TSE and SA-RBF-TSE on Measurement noise standard deviation σ LOS. |
 |
Fig. (5) Number of hidden layer nodes for RBF-TSE and SA-RBF-TSE on NLOS error σNLOS. |
CONCLUSION
In this paper, a Novel Positioning Algorithm is proposed. The algorithm using Self-Adaptive RBF neural network algorithm to correct TDOA measurements, then Taylor algorithm adopted the revised TDOA value to improve the position estimation. It shows that the proposed Positioning algorithm has a strong inhibition of LOS/NLOS error of simulation results. Through the neural network of the LOS/NLOS error correction in NLOS channel environment, this algorithm has high location accuracy and reliability of the positioning performance is better than Taylor algorithm, LS algorithm, Chan algorithm and RBF-TSE algorithm, and the required Hidden layer nodes for getting performance threshold are less than the RBF-TSE algorithm.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was supported by 2013 Technology Foundation for Selected Overseas Chinese Scholar (No.401053740756), Ministry of Personnel of Beijing and The Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry and Training program for Outstanding Young Scholars (No.14085), 2016 annual “Outstanding Young Teacher Training Program” project of North China University of Technology
REFERENCES
| [1] | L.M. Winternitz, W.A. Bamford, and G.W. Heckler, "A GPS receiver for high-altitude satellite navigation", IEEE J. Sel. Top. Signal Process., vol. 3, no. 4, pp. 541-556, 2009. [http://dx.doi.org/10.1109/JSTSP.2009.2023352] |
| [2] | M. Soltanian, A.M. Pezeshk, and A. Mahdavi, "A new iterative position finding algorithm based on Taylor series expansion", In: Proceedings of 2011 19th Iranian Conference on Electrical Engineering(ICEE), Maryam, Dallali, 2011, pp. 1-4. |
| [3] | X. J. Yu, and W. Wei, "A new TDOA location technique based on Taylor series expansion in cellular networks", In: Proceedings of the 4th International Conference on Parallel and Distributed Computing, Applications and Technologie, Chengdu, China, 2003, pp. 378-381. |
| [4] | T. G. Hua, D. Jing, and N. C. Jian, "Series type of neural network and its application and research in forecasting of river floods", Res. Water Resources., vol. 24, no. 2, pp. 4-5, 2003. |
| [5] | C.X. Yun, M. Qiang, and T. Alkharobi, "New neural networks based on Taylor series and their research", In: Proceedings of 2nd IEEE International Conference on Computer Science and Information Technology., Beijing, China, 2009, pp. 291-194. |
| [6] | W.L biao, and F Jian, "Study of self-adaptive RBF neural network control method for the engine idle speed control", In: Proceedings of 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet)., XianNing, China, 2011, pp. 2633-2636. |
| [7] | K. Meng, Z.Y. Dong, D.H. Wang, and K.P. Wong, "A self-adaptive RBF neural network classifier for transformer fault analysis", IEEE Trans. Power Syst., vol. 25, no. 3, pp. 1350-1360, 2010. [http://dx.doi.org/10.1109/TPWRS.2010.2040491] |
| [8] | P. Singh, and S. Agrawal, "TDOA based node localization in WSN using neural networks", In: Proceedings of 2013 International Conference on Communication Systems and Network Technologies (CSNT), Gwalior, India, 2013, pp. 400-404. [http://dx.doi.org/10.1109/CSNT.2013.90] |
| [9] | Y. Kegen, Y.J. Guo, and I. Oppermann, "Modified taylor series expansion based positioning algorithms", In: Proceedings of IEEE Vehicular Technology Conference, Singapore, 2008, pp. 2656-2660. |
| [10] | C.Y. Tong, T.W. Yue, S.H. Cheung, and C.P. Chung, "Time-of-arrival based localization under NLOS conditions", IEEE Transactions Vehicular Technology, vol. 55, no. 1, pp. 17-24, 2006. [http://dx.doi.org/10.1109/TVT.2005.861207] |




