- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mechanical Engineering Journal
(Discontinued)
ISSN: 1874-155X ― Volume 14, 2020
Minimal Structural ART Neural Network and Fault Diagnosis Application of Gas Turbine
Qingyang Xu*
Abstract
Adaptive Resonance Theory (ART) model is a special neural network based on unsupervised learning which simulates the cognitive process of human. However, ART1 can be only used for binary input, and ART2 can be used for binary and analog vectors which have complex structures and complicated calculations. In order to improve the real-time performance of the network, a minimal structural ART is proposed which combines the merits of the two models by subsuming the bottom-up and top-down weight. The vector similarity test is used instead of vigilance test. Therefore, this algorithm has a simple structure like ART1 and good performance as ART2 which can be used for both binary and analog vector classification, and it has a high efficiency. Finally, a gas turbine fault diagnosis experiment exhibits the validity of the new network.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 13
Last Page: 22
Publisher Id: TOMEJ-10-13
DOI: 10.2174/1874155X01610010013
Article History:
Received Date: 17/02/2014Revision Received Date: 21/03/2015
Acceptance Date: 09/06/2015
Electronic publication date: 15/3/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the School of Mechanical, Electrical & Information Engineering, Shandong University (Weihai), Weihai, 264209, P.R. China; Tel: 86-0631-5688338; Fax: 86-0631-5688338; E-mail: qingyangxu@sdu.edu.cn
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 17-02-2014 |
Original Manuscript | Minimal Structural ART Neural Network and Fault Diagnosis Application of Gas Turbine | |
1. INTRODUCTION
Adaptive Resonance Theory (ART) architecture is a special neural network inspired by the human cognitive information processing [1G.A. Carpenter, and S. Grossberg, "The ART of adaptive pattern recognition by a self-organizing neural network", Computer, vol. 21, no. 3, pp. 77-88, 1988.
[http://dx.doi.org/10.1109/2.33] ]. ART first emerged to overcome the instabilities inherent in feed-forward neural network using supervised learning algorithms, such as a back propagation network, a sample set is learned sequentially until the learning is completed. When a new pattern is presented to the network, the network has to be completely retrained with all of the patterns. If the network learns the new pattern alone, it will forget the previous learning. The ability to learn a new pattern is the plasticity of a network, and the ability of learning without being affected by the previous learning is the stability of a network [2G.A. Carpenter, S. Grossberg, and D.B. Rosen, "ART2-A: an adaptive resonance algorithm for rapid category learning and recognition", Neural Netw., vol. 4, no. 4, pp. 493-504, 1991.
[http://dx.doi.org/10.1016/0893-6080(91)90045-7] ]. ART is designed to solve the dilemma of stability and plasticity.The neural network is stable enough to preserve the past learning information, but it is adaptable enough to learn the new information [1G.A. Carpenter, and S. Grossberg, "The ART of adaptive pattern recognition by a self-organizing neural network", Computer, vol. 21, no. 3, pp. 77-88, 1988.
[http://dx.doi.org/10.1109/2.33] ]. The ART theory has since led to an evolving series of models for unsupervised pattern learning and recognition. ART1 is designed for binary vectors clustering, ART2 for continuousvectors and ART3 can realize parallel search and hypothesis testing of distributed recognition in the multilevel network [3G.A. Carpenter, and S. Grossberg, "ART3 hierarchical search using chemical transmitters in self-organizing pattern recognition architectures", Neural Netw., vol. 3, no. 2, pp. 129-152, 1990.
[http://dx.doi.org/10.1016/0893-6080(90)90085-Y] ], which has two complex structure. These models are capable of learning and recognizing arbitrary input.
ART1 is a simple neural network that can recognize binary vectors only. In practical, the data is always analog value. ART2 can be used as analog value. However, ART2 has a complex structure to realize real-time calculation. Therefore, we want to design a new algorithm combing the ART1 and ART2. According to the theory of ART, we simplify the structure of ART1 and add vector similarity check to the new algorithm in order to provide a high efficiency ART1 algorithm with minimal structure for data recognition.
This paper is organized as follows. In section 2, kinds of ART models are presented. In section 3, the algorithm of ART1 is discussed, and the minimal structural ART is presented. Section 4 presents a gas turbine diagnosis experiment. Some conclusions are reported in section 5.
2. KINDS OF ART MODELS
The ART1 was the first ART model, which was designed for recognizing binary input originally. The ART1 have two processes by bottom-up weight W and top-down weight T, and another vigilance test part ρ [4G.A. Keskin, S.I. Sevin, and C. Ozkan, "The fuzzy ART algorithm: a categorization method for supplier evaluation and selection", Expert Syst. Appl., vol. 37, no. 2, pp. 1235-1240, 2010.
[http://dx.doi.org/10.1016/j.eswa.2009.06.004] ]. It is the base of ART-MAP. ART-MAP model has two unsupervised modules to carry out supervised learning that can rapidly realize a stable categorical mapping between m-dimensional vectors and n-dimensional vectors [5G.A. Carpenter, S. Grossberg, and J.H. Reynolds, "ARTMAP supervised real-time learning and classification of nonstationary data by a self-organizing neural network", Neural Networks, vol. 4, pp. 565-588, 1991.
[http://dx.doi.org/10.1109/ICNN.1991.163370] ]. Fig. (1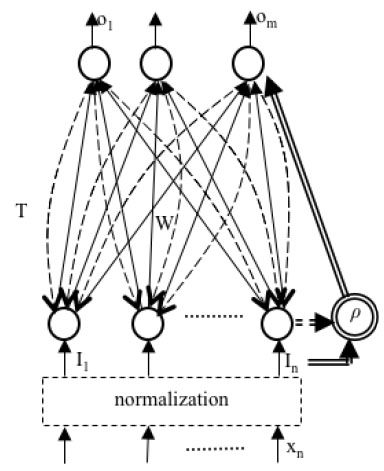 ) is the structure of ART-MAP.
) is the structure of ART-MAP.
 |
Fig. (1) The structure of ART-MAP. |
ART2, which was designed for recognizing analog input, employed a computationally expensive architecture and difficult parameter selection. Fig. (2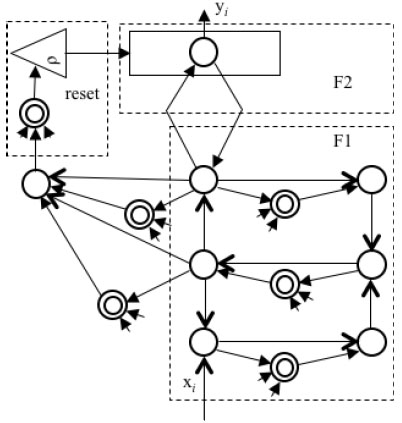 ) is the structure of ART2. The ART2 have F1 and F2 processes to recognize categories stablyin response to both analog and binary input patterns [2G.A. Carpenter, S. Grossberg, and D.B. Rosen, "ART2-A: an adaptive resonance algorithm for rapid category learning and recognition", Neural Netw., vol. 4, no. 4, pp. 493-504, 1991.
) is the structure of ART2. The ART2 have F1 and F2 processes to recognize categories stablyin response to both analog and binary input patterns [2G.A. Carpenter, S. Grossberg, and D.B. Rosen, "ART2-A: an adaptive resonance algorithm for rapid category learning and recognition", Neural Netw., vol. 4, no. 4, pp. 493-504, 1991.
[http://dx.doi.org/10.1016/0893-6080(91)90045-7] ]. The F1 field of ART2 is more complex than ART1 becausethe continuous-valued input vectors may be arbitrarily close to each other. The F1 field in ART2 contains the normalization and noise filtering operations with complex structure. The F2 field outputs the classification result. In addition, there is a reset mechanism to have a comparison of the bottom-up input signals and top-down learned information.
 |
Fig. (2) The structure of ART2 neural network. |
These networks recognize inputs by unsupervised learning which is the advantaged feature of ART models [6A. Baraldi, and E. Alpaydin, "Constructive feedforward ART clustering networks. I", IEEE Trans. Neural Netw., vol. 13, no. 3, pp. 645-661, 2002.
[http://dx.doi.org/10.1109/TNN.2002.1000130] [PMID: 18244462] ], notably, the pattern matching of input with the learned prototype vectors. This matching process leads either to a resonant state that focuses attention and triggers stable prototype learning or to a self-regulating parallel memory search [7Z. Chen, Z. Cai, Z. Li, and X. Wang, "The influence of ART1 parameters setting on the behavior of layer 2", In: Proceedings of the 4th International Conference on Machine Learning and Cybernetics, Guangzhou, China, 2005, pp. 4805-4808.]. If the algorithm selects an established category in the searching process, then the learning information will be reinforced by the new input pattern. If an untrained node is selected by the searching process, then a new node will represent the new category. However, different models have different performance. ART1 is always used for binary input, and ART2 can be used to analog input too but with complex structures. In this paper, we want to combine the simple structure of ART1 with good performance of ART2.
3. MINIMAL STRUCTURAL ART
The basic architecture of ART1 and ART2 network involves two layers: input layer (F1 layer), competition layer (F2 layer), and another reset mechanism. The F1 layer combines signals from the input and the F2 layer to carry out vigilance test. The matching process leads either to a resonant state or to a parallel memory search. However, the two models are different in this section that ART2 has a more complex computation process than ART1. If the algorithm selects an established category in the searching process, then the learning information will be reinforced by the new input pattern. If an untrained node is selected by the searching process, then a new category establishes.
There are two connections between the layers F1 and F2. W denotes the bottom-up weights from F1 to F2 and T denotes the top-down weights from F2 to F1. The processing of ART-based models is that the input vectors are transported to F1 layer after normalization or not, then the value pass to F2 layer bywij, select the maximum output neuron in F2 layer, and make use of the tij of this neuron and input vectors carrying out vigilance test. There are two typical processes bottom-up and top-down. In the Fuzzy ART, a view is acknowledged by Carpenter, Grossberg & Rosen [8G.A. Carpenter, S. Grossberg, and D.B. Rosen, "Fuzzy ART fast stable learning and categorization of analog patterns by an adaptive resonance system", Neural Netw., vol. 4, no. 6, pp. 759-771, 1991.
[http://dx.doi.org/10.1016/0893-6080(91)90056-B] ], the weight vector wj can subsume both the bottom-up weight and top-down weight vectors of ART1. Therefore, according to this theory, we subsume both the bottom-up weight and top-down weight, which can simplify the process of data cluster without top-down calculation. However, we do not adopt the vigilance test method of ART1. We adopt the vector similarity check like ART2 in vigilance test in order to recognize arbitrary input mode. The victorious neuron is the neuron with maximum output and with bigger than ρ in F2 layer. Fig. (3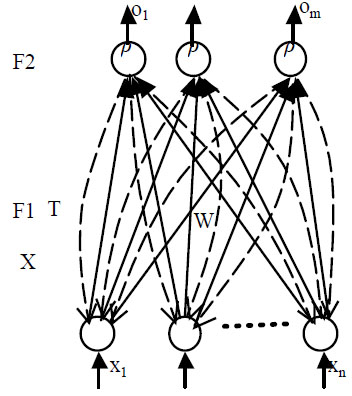 ) is the diagram of minimal structural ART.
) is the diagram of minimal structural ART.
 |
Fig. (3) The structure of minimal structural ART. |
3.1. The New Minimal Structural ART Algorithm
The minimal structural ART algorithm combines the merit of ART1 and ART2. The structural of the network is more like ART1, and the learning process is more like the ART2 which uses the vector similarity test.
The concrete algorithm of the new ART1 is shown as follows.
Step 1. Initialize the weights from F1 layer to F2 layer with the same small value.
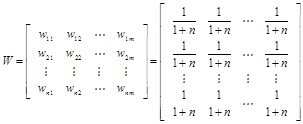 |
(1) |
wij is the forward connection weight of ith input neuron and the jth output neuron, n is the number of input neuron, m is the output neuron number, m may be the same as sample number.
The vigilance parameter ρ is set to a value of 0-1 for vigilance test which influences the precision of recognition.
Step 2. Input pattern set X. X is the sample data.
 |
(2) |
xmn denates mth input of nth group input, n is neuron number, m is sample number.
Step 3. Compute the neuron output of F2 layer and do the competition of output neuron which is different from the conventional ART1.
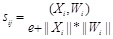 |
(3) |
sij is the cosine of vector angle. It does not indicate the similarity of vector length. Therefore, we also should do the length test of vector.
Define X=(x1, x2, …xn),Y=(y1, y2, …yn)
Then (X, Y)= (x1 y1+x2 y2, …+xn yn)
The vector norm is done as following:
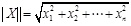 |
(4) |
The similarity of vectors is
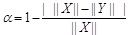 |
(5) |
Therefore, the similarity of vector X and Y is r=α*sinstead of s.
Select the optimal matching neuron.
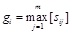 |
(6) |
Step 4. Vigilance test. If sig>ρ, acknowledge the recognition result, and adjust the weight according to the following equation.
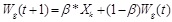 |
(7) |
If there is no matching neuron, then create a new cluster center for the new sample. β is the learning rate of the network. If β=1 in sample learning, it is the fast learning type.
In order to encode the noisy input sets efficiently, ρ is always set to 1 when number J is an uncommitted node. The ρ will be smaller than 1 after the category is committed. After a new category J becomes active, Wjnew=I.
In the new network, we make use of the structure merits of the ART1 and vector testing mechanism of the ART2, and construct a minimal structural ART(MSART) neural network to classify the data.
3.2. Classification Stability Analysis of MSART
For the same input, the stability analysis of identification is as follows. According equation (7),
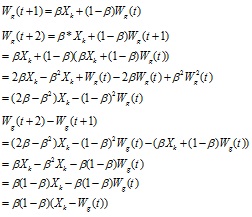 |
When g is an uncommitted node, β is set to 1 in training process, then Wg= Xk. Therefore, the learning of neural network is stable.
For different input, the stability analysis of identification is as follows.
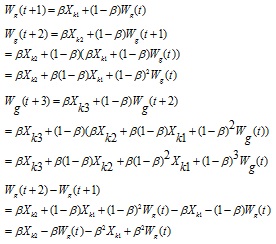 |
According to initialization, when the sample is Xk1, thenWg(t)= Xk1, so the previous equation can be simplified as:
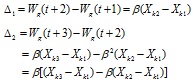 |
Xk1 is the initial sample, and Δ1 and Δ2 indicate the degree of shifting from cluster center to Xk2 and Xk3. If β is zero, the cluster center will not shift; it will have obvious shifting with bigger β. If β is one, it will return the fast learning of ART1, and then the cluster center will move to Xk2. The value of β decides the adaptation degree from memorized center to the new one. From Δ2 we can see the neural network will obtain the cluster center according to the new input Xk3 and previous input Xk1 and Xk2 when there is different input.
4. FAULT DIAGNOSIS EXPERIMENT
ART1 is always used to fault diagnosis [9S. Rajakarunakaran, P. Venkumar, D. Devaraj, and K.S. Rao, "Artificial neural network approach for fault detection in rotary system", Appl. Soft Comput., vol. 8, no. 1, pp. 740-748, 2008.
[http://dx.doi.org/10.1016/j.asoc.2007.06.002] -12M. Wang, and T. Zan, "Adaptively pattern recognition in statistical process control using fuzzy ART neural network", In: International Conference on Digital Manufacturing and Automation (ICDMA), Beijing, China, 2010, pp. 160-163.
[http://dx.doi.org/10.1109/ICDMA.2010.263] ]. For application, we use the minimal structural ART1 for fault diagnosis of gas turbine. Gas turbine is a large rotating machinery of power plant, provided with an air compressor and a combustion chamber. It is one of the most important equipment of power generation ensuring its normal operation is very important. Vibration amplitude is usually adopted to diagnose the fault of the machine. A wavelet transform (WT) analyze the signal in time and frequency domain. The advantage of wavelet transform is the ability of characterizing the local features of the signal. It is useful for analyzing the vibration signal of rotating machinery with faults. WT is used to analyze the vibration signal of gas turbine. The fault diagnosis process is shown by Fig. (4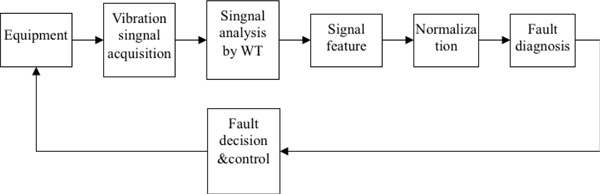 ).
).
 |
Fig. (4) The flowchart of gas turbine fault diagnosis. |
The feature of fault distributes on the eight or nine frequency bands. The common faults are rotor imbalance, pneumatic couple, misalignment of rotor, oil whirl, the rotor radial rub, coexistence loosening, thrust bearing damage, surging, bearing pedestal loosening, varying bearing stiffness. Therefore, we use the typical feature data of the fault to train the network. The following Table 1 is the fault feature data of gas turbine. The data in the table is the data after normalization. We use the minimal structural ART to diagnose the fault and also to test the validity of network.
The parameter ρ is 0.99, β is 1, the input neuron number is 8, and the output neuron number is 15 in the training process. After the training of the neural network, the ten fault samples are stored. The three dimensional contrast figure of network stored information and samples are shown in Figs. (5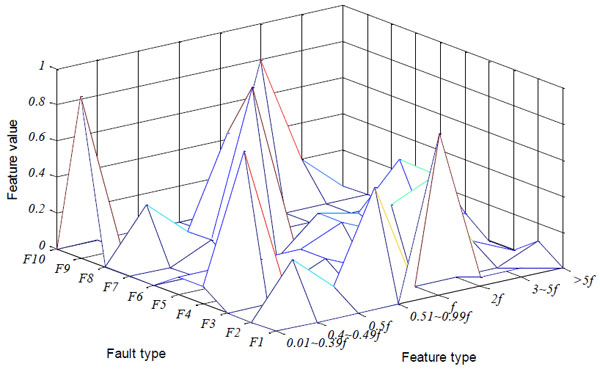 , 6
, 6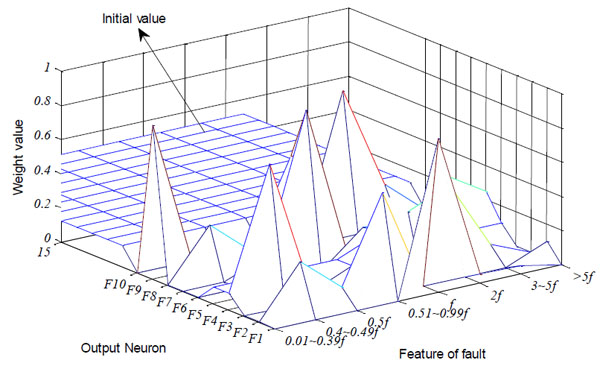 ), and the isoline maps are shown in Figs. (7
), and the isoline maps are shown in Figs. (7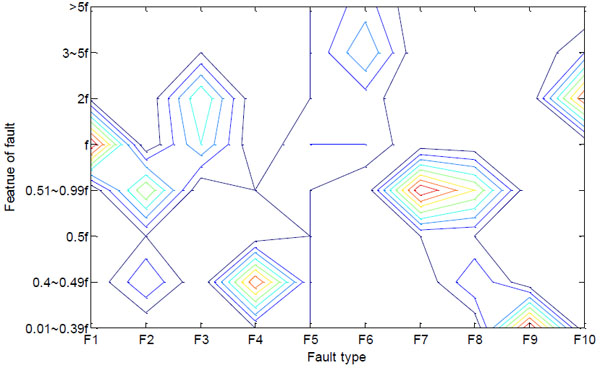 , 8
, 8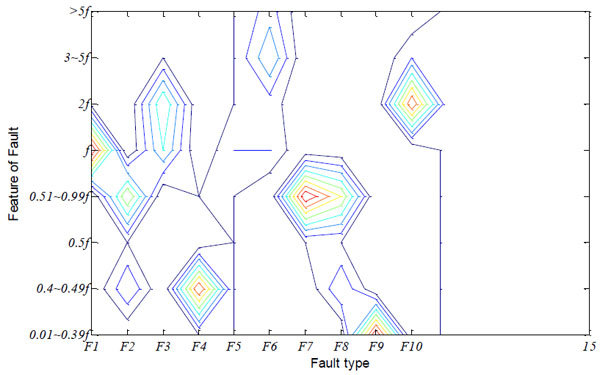 ). The features of the fault are shown clearly in the figures.
). The features of the fault are shown clearly in the figures.
 |
Fig. (5) The three dimensional diagram of sample. |
 |
Fig. (6) The three dimensional diagram of storage weight. |
In the neural network, the output neural number is 15. From the three dimensional figure and isoline map of sample, we can see F2 and F8 have similar features, and this is why the parameter ρ has a larger value of 0.99 to recognize it. Ten output neurons learn the sample data, and others are unused.
If the ρ is smaller than 0.99, the neural network will not distinguish F2 and F8 as shown in Table 2. The following table is the neural network training result when ρ=0.95. The neural network mistakes F8 for F2.
Take a gas turbine of certain power plant for example, the vibration data is gathered and has a WT to extract the signal features [13C. Limin, X. Zhijiang, L. Liyun, and S. Hongyan, "Vibration fault diagnosis of steam turbine using immune genetic neural networks", J. Vib. Meas. Diagnosis, vol. 30, no. 6, pp. 675-678, 2010., 14X. San-mao, "The study of fault intelligent diagnosis for turbine based on gray relational degree", Turbine Technol., vol. 51, no. 6, pp. 465-467, 2009.]. Then, the data is shown in Table 3 after the normalization.
The neural network has learned ten types of fault. When input is the E1, the output of the neurons are [0.9990.0090.6610.0010.6280.4050.011 0.0090.058 0.384 0.384 0.384 0.384 0.384]. Then, the diagnosis result is given out after having a vigilance test. The fault type is F1. The neurons output are [0.654 0.093 0.976 0.196 0.728 0.616 0.006 0.093 0.018 0.772 0.641 0.641 0.641 0.641 0.641] when the E2 is presented to the network. The fault type is F3 according to the neural network diagnosis result. The experiment data E1 and E2 as shown in Table 4 have a comparison with the corresponding sample data and data of w storage in Figs. (9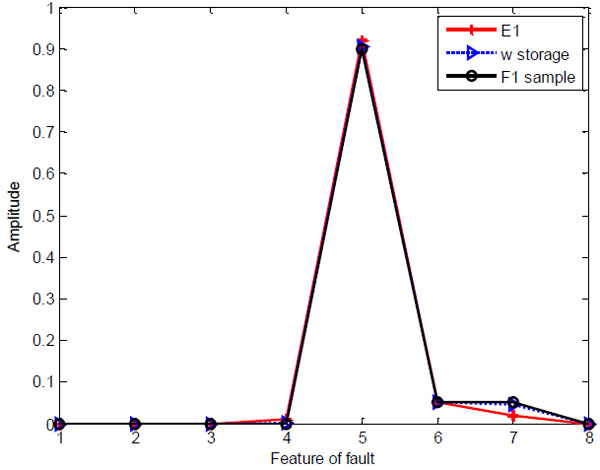 , 10
, 10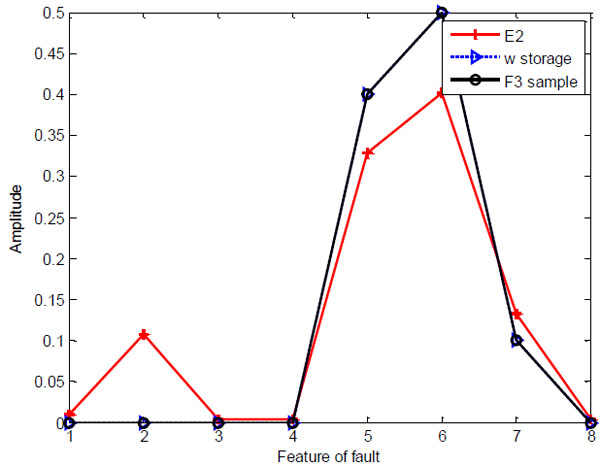 ).
).
 |
Fig. (7) The isoline diagram of sample. |
 |
Fig. (8) The isoline diagram of storage weight. |
 |
Fig. (9) The comparison diagram of E1, storage weight and F1. |
 |
Fig. (10) The comparison diagram of E2, storage weight and F3. |
CONCLUSION
In this paper, we propose a minimal structural ART, which combines the bottom-up vectors withthe top-down weight vectors of ART1. The new neural network can recognize both the binary and analog values, and has less amount of calculation. Therefore, we use a better vigilance test method. The vector similarity checking method of ART2 is introduced here, which overcomes the drawback of ART1. A common gas turbine fault diagnosis example is used to test the new algorithm. The sample data about the feature of frequency is learned by the network. The gas turbine diagnosis experiment exhibits its validity in recognizing the fault.
CONFLICT OF INTEREST
The author confirms that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was supported in part by the National Natural Science Foundation of China under Grant No. 61174044, Natural Science Foundation of Shandong Province under Grant No. ZR2015PF009 and Independent Innovation Foundation of Shandong University under grant No. 2015ZQXM002
REFERENCES
| [1] | G.A. Carpenter, and S. Grossberg, "The ART of adaptive pattern recognition by a self-organizing neural network", Computer, vol. 21, no. 3, pp. 77-88, 1988. [http://dx.doi.org/10.1109/2.33] |
| [2] | G.A. Carpenter, S. Grossberg, and D.B. Rosen, "ART2-A: an adaptive resonance algorithm for rapid category learning and recognition", Neural Netw., vol. 4, no. 4, pp. 493-504, 1991. [http://dx.doi.org/10.1016/0893-6080(91)90045-7] |
| [3] | G.A. Carpenter, and S. Grossberg, "ART3 hierarchical search using chemical transmitters in self-organizing pattern recognition architectures", Neural Netw., vol. 3, no. 2, pp. 129-152, 1990. [http://dx.doi.org/10.1016/0893-6080(90)90085-Y] |
| [4] | G.A. Keskin, S.I. Sevin, and C. Ozkan, "The fuzzy ART algorithm: a categorization method for supplier evaluation and selection", Expert Syst. Appl., vol. 37, no. 2, pp. 1235-1240, 2010. [http://dx.doi.org/10.1016/j.eswa.2009.06.004] |
| [5] | G.A. Carpenter, S. Grossberg, and J.H. Reynolds, "ARTMAP supervised real-time learning and classification of nonstationary data by a self-organizing neural network", Neural Networks, vol. 4, pp. 565-588, 1991. [http://dx.doi.org/10.1109/ICNN.1991.163370] |
| [6] | A. Baraldi, and E. Alpaydin, "Constructive feedforward ART clustering networks. I", IEEE Trans. Neural Netw., vol. 13, no. 3, pp. 645-661, 2002. [http://dx.doi.org/10.1109/TNN.2002.1000130] [PMID: 18244462] |
| [7] | Z. Chen, Z. Cai, Z. Li, and X. Wang, "The influence of ART1 parameters setting on the behavior of layer 2", In: Proceedings of the 4th International Conference on Machine Learning and Cybernetics, Guangzhou, China, 2005, pp. 4805-4808. |
| [8] | G.A. Carpenter, S. Grossberg, and D.B. Rosen, "Fuzzy ART fast stable learning and categorization of analog patterns by an adaptive resonance system", Neural Netw., vol. 4, no. 6, pp. 759-771, 1991. [http://dx.doi.org/10.1016/0893-6080(91)90056-B] |
| [9] | S. Rajakarunakaran, P. Venkumar, D. Devaraj, and K.S. Rao, "Artificial neural network approach for fault detection in rotary system", Appl. Soft Comput., vol. 8, no. 1, pp. 740-748, 2008. [http://dx.doi.org/10.1016/j.asoc.2007.06.002] |
| [10] | L. Massey, "On the quality of ART1 text clustering", Neural Netw., vol. 16, no. 5-6, pp. 771-778, 2003. [http://dx.doi.org/10.1016/S0893-6080(03)00088-1] [PMID: 12850033] |
| [11] | T. Barszcz, M. Bielecka, A. Bielecki, and M.W. Jcik, "Wind turbines states classification by a fuzzy-ART neural network with a stereographic projection as a signal normalization", In: Lecture Notes in Computer Science, vol. 6594. 2011, pp. 225-234. [http://dx.doi.org/10.1007/978-3-642-20267-4_24] |
| [12] | M. Wang, and T. Zan, "Adaptively pattern recognition in statistical process control using fuzzy ART neural network", In: International Conference on Digital Manufacturing and Automation (ICDMA), Beijing, China, 2010, pp. 160-163. [http://dx.doi.org/10.1109/ICDMA.2010.263] |
| [13] | C. Limin, X. Zhijiang, L. Liyun, and S. Hongyan, "Vibration fault diagnosis of steam turbine using immune genetic neural networks", J. Vib. Meas. Diagnosis, vol. 30, no. 6, pp. 675-678, 2010. |
| [14] | X. San-mao, "The study of fault intelligent diagnosis for turbine based on gray relational degree", Turbine Technol., vol. 51, no. 6, pp. 465-467, 2009. |