- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mechanical Engineering Journal
(Discontinued)
ISSN: 1874-155X ― Volume 14, 2020
Research on Sealing Properties and its Influence Factors of Spherical Mechanical Seal Based on ANSYS
Xuhui Zhou, Zhenglin Liu*, Li Zou, Xingxin Liang, Huanjie Wang, Jun Yang
Abstract
When a marine stern shaft is bent with shafting misalignment and stern bearing wear factors, etc., the sealing properties of a plane mechanical seal is declined with the increase of both contact pressure and temperature of sealing surface, so a spherical mechanical seal which can automatically adjust the contact state of sealing surfaces is proposed to replace the plane mechanical seal in order to solve the aforementioned problems. The sealing properties of a spherical mechanical seal is directly influenced by the sealing structure size such as sealing spherical radius, the distance between stator and rotary ring seats, inner and outer diameters of stator ring. The thermal-structure coupling model of the spherical mechanical seal in underwater vehicles is built with ANSYS finite element method, and the influence of structure size on the sealing performances of the spherical mechanical seal is discussed. The study results show that as spherical radius is increased, the contact region of spherical sealing surfaces is decreased and the opening region is expanded, and the highest temperature and maximum contact pressure on the spherical sealing surfaces are raised. As inner or outer diameter of stator ring is increased, the maximum contact pressure of the former is raised, and one of the latter is declined, but the highest temperatures of both on sealing surfaces are enhanced linearly. When the distance between static and rotary ring seats is increased, the highest temperature of sealing surface and maximum contact pressure are increased in a nonlinear way. These conclusions are of important theoretical significance and engineering application value for the structure optimization of spherical mechanical seals in vessels, particularly underwater vehicles.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 160
Last Page: 172
Publisher Id: TOMEJ-10-160
DOI: 10.2174/1874155X01610010160
Article History:
Received Date: 17/12/2015Revision Received Date: 07/07/2016
Acceptance Date: 10/07/2016
Electronic publication date: 30/09/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the School of Energy and Power Engineering, Wuhan University of Technology, 1040 Heping Road, Yujiatou Campus, Wuhan 430063, People’s Republic of China; Tel: 00865-51239638; Fax: 86533886; E-mail: zlliu812@163.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 17-12-2015 |
Original Manuscript | Research on Sealing Properties and its Influence Factors of Spherical Mechanical Seal Based on ANSYS | |
1. INTRODUCTION
Stern shaft mechanical seal is an important device which seriously influences both safety and survival ability of underwater vehicles. Once the mechanical seal fails, disastrous consequences will be brought about. At present, in underwater vehicles the plane mechanical sealing devices of stern shafts are ordinarily adopted, whose sealing performances are mainly depended on the sealing structure size, materials of both stator and rotary rings and the contact state of the sealing friction pair. In general, stator ring one graphite carbon, and rotary ring material is hard alloy. Under normal operation condition, both stator and rotary rings of the device generally are in mixed friction state. But the actual mechanical seal is a complex dynamic system which is sensitive to sealing structure size, installation and manufacturing error, especially for sealing structure size. The sealing structure size can impact on sealing properties such as temperature, contact pressure and deformation of the seal. Therefore, the optimization of sealing structure size of a mechanical seal is extremely important.
In researches of mechanical seal, a number of domestic and oversea companies, such as Ningbo Vulcan Mechanical Seal Manufacture Co., Ltd., America Durametallic Co., British Deep Sea Seal Ltd., Japanese Eagle Company, have made a lot of research work, and achieved great progress. But for some reason such as shafting misalignment and vibration, the clearance between stern shaft and stern bearing, serious wear of stern bearings and sinking or bending of stern shafts, plane mechanical sealing element appears radial runout at working so that high local contact pressure and temperature, lager deformation and overrun leakage are brought about. This makes both safety and reliability of underwater vehicles be affected seriously.
Zhang Zhenguo, et al. [1Z.G. Zhang, S.W. Yao, and X.H. Zhou, "Research on mechanical deformation of friction pair of stern shaft sealing device in submarine under great depth", Ocean Eng., no. 6, pp. 12-14, 2004.] investigated the sealing-coupling problems of the stern shaft seal, their research results indicate that both stator and rotary rings will be distorted under the imbalance force or moment. It has great influence on the sealing performance in a particular case such as high revolution and submergence depth. In Andre Parfait's researches [2A.P. Nyemeck, N. Brunetière, and B. Tournerie, "A multiscale approach to the mixed lubrication regime: application to mechanical seals", Tribol. Lett., vol. 47, pp. 417-429, 2012.
[http://dx.doi.org/10.1007/s11249-012-9997-5] , 3A.P. Nyemeck, N. Brunetière, and B. Tournerie, "Parametric study of the behavior of a mechanical face seal operating in mixed and TEHD lubrication regimes", In: Proceedings of the ASME 11th Biennial Conference on Engineering Systems Design and Analysis, ESDA2012, Nantes, France, 2012.
[http://dx.doi.org/10.1115/ESDA2012-82743] ], calculating model and conversion method of mixed lubrication region, heat conduction and deformation theories were used to solve the fluid-solid coupling problem of plane mechanical seal. Christophe Minet [4C. Minet, N. Brunetière, and B. Tournerie, "A deterministic mixed lubrication model or mechanical seals", J. Tribol., vol. 133, no. 4, p. 042203, 2011.
[http://dx.doi.org/10.1115/1.4005068] ] pointed out that the mixed lubrication of the mechanical seal is more complex, and the reports on the test investigation of mechanical seal are only few. Philips et al. [5R.L. Phillips, L.E. Jacobs, and P. Merati, "Experimental determination of the thermal characteristics of a mechanical seal and its operating environment", Tribol. T., vol. 40, pp. 559-568, 1997.
[http://dx.doi.org/10.1080/10402009708983693] ] experimentally analyzed the impact of thermal distortion of mechanical seal faces on seal performance. The seal face torque, thermal gradients, and fluid flow patterns under the normal operating conditions of the seal were measured. Nusselt numbers and heat generation were calculated from the measured data. Pascovici and Etsion [6M.D. Pascovici, and I. Etsion, "A thermo-hydrodynamic analysis of a mechanical face seal", J. Tribol., vol. 114, pp. 639-645, 1992.
[http://dx.doi.org/10.1115/1.2920930] ] studied the thermo-hydrodynamic behavior of a mechanical face seal. The most important effects caused by the thermal environment are radial taper and waviness thermally induced. Liu Wei, et al. [7W. Liu, Y. Liu, and J.J. Zhai, "Three-dimensional flow–heat coupling model of a wavy-tilt-dam mechanical seal", Tribol. Trans., vol. 56, no. 6, pp. 1146-1155, 2013.
[http://dx.doi.org/10.1080/10402004.2013.812758] ] established a three-dimensional flow-heat coupling model of a wavy-tilt-dam (WTD) mechanical seal to study the heat transfer in both the fluid and the solid domains. The inlet temperature boundary condition was discussed and two modified inlet boundary condition methods were proposed to eliminate the noncontinuity of the film inlet temperature. According to a lot of experiment, Etsion, et al. [8I. Etsion, Y. Kligerman, and G. Halperin, "Analytical and experimental investigation of laser-textured mechanical seal faces", Tribol. Trans., vol. 42, no. 3, pp. 511-516, 1999.
[http://dx.doi.org/10.1080/10402009908982248] , 9I. Etsion, and G. Halperin, "A laser surface textured hydrostatic mechanical seal", Tribol. Trans., vol. 45, no. 3, pp. 430-434, 2002.
[http://dx.doi.org/10.1080/10402000208982570] ] had done many experiments to investigate the effect of laser surface texturing (LST) on mechanical seals. Marius Pustan, et al. [10M. Pustan, O. Belcin, and C. Birleanu, "Mechanical seals with oscillating stator", Meccanica, vol. 48, pp. 1191-1200, 2013.
[http://dx.doi.org/10.1007/s11012-012-9660-0] ] presented theoretical analyses and experimental investigations of the mechanical seal subjected to axial impulses of the stator ring. The study results indicated that the amplitude of oscillations of the stator ring depends on the pressure of sealed fluid. Richard F. Salant, et al. [11R.F. Salant, and B. Cao, "Unsteady analysis of a mechanical seal using Duhamel’s method", J. Tribol., vol. 127, no. 3, pp. 623-631, 2005.
[http://dx.doi.org/10.1115/1.1924427] ] developed the unsteady numerical model of the mechanical seal with mixed lubrication. The thermal analysis is performed using Duhamel’s method in combination with a lot of experiments to determine Duhamel’s auxiliary function. The results gained with this semiempirical approach were agreed with those of a finite element analysis. The model had been used to predict the performance of a mechanical seal during startup and shutdown.
Overseas, the theoretical analysis foundation for the deformation and temperature fields of plane mechanical seal has been established, and the coupling theory and experimental research are mainly paid attention to now. At home, the solutions of both deformation and temperature fields are still emphasized. Xudong Peng, et al. [12X.D. Peng, W. Liu, and S.X. Bai, "Effects analysis of thermo-elastic deformation on the performance of hydrostatic mechanical seals in reactor coolant pumps", J. Mechl. Eng., vol. 46, no. 23, pp. 146-153, 2010.
[http://dx.doi.org/10.3901/JME.2010.23.146] ] established a steady heat transfer model for a hydrostatic face seal with convergence gap, studied the effects of thermo-elastic deformation on the performance of hydrostatic mechanical seals in reactor coolant pumps. Their investigations demonstrated that thermo-elastic deformation of a hydrostatic mechanical seal used in reactor coolant pumps could severely affect sealing performance under the operation conditions such as high-pressure, high-speed and in a wide temperature range. Qin Bo, et al. [13B. Qin, Z.L. Liu, and X.H. Zhou, "Research on influence of dam seal structure on performance of marine mechanical seal", In: Improving Multimodal Transportation Systems - Information, Safety, and Integration - Proceedings of the 2nd International Conference on Transportation Information and Safety, ACS: United States. 2013, pp. 2259-2264.
[http://dx.doi.org/10.1061/9780784413036.303] ] deemed that the structure of the narrow face mechanical seal of marine stern shaft is usually superior to the wide face seal because dam seal structure can reduce the highest temperature, the maximum contact pressure, the deformation and the seal gap of the narrow sealing face, but the width of sealing surface shall be optimized further. Zhu Xueming [14X.M. Zhu, "Research on Numerical Analysis and Optimization of Mechanical Sealing Performance", M.s. thesis, Wuhan University of Technology, Wuhan, China, 2005.] made the thermal-structure field coupling analysis of mechanical seal rings directly in steady state, and took the emulating calculations of stress, temperature and deformation.
So far, both domestic and foreign researches on the structure and optimization of mechanical seals are mainly concentrated on plane mechanical seals which are sensitive to sealing structure size, installation technique and manufacturing errors. In a certain operation stage, the sealing surface deflection of plane mechanical seal is almost inevitable. In case of kind of phenomenon, the fundamental change of dynamic performances of the seal will be happened, and the sealing state is deviated from the design goals, which leads to the early damage of the seal. So the special sealing device, such as a spherical mechanical seal, can be used to solve the practical problems in deep submergence engineering in order to improve the sealing properties of the mechanical seals.
2. SPHERICAL MECHANICAL SEAL COMPOSITION
The contact status of spherical mechanical seal is difference from one of plane mechanical seal. The sealing surface of the former is spherical surface and the latter is plane surface. Spherical mechanical seal can automatically adjust the contact state of sealing surfaces, enhance the following features of sealing friction pair, always keep spherical sealing surfaces of both stator and rotary rings in contact state, prevent the plane mechanical seal’s opening generated with the stern shaft deformation (offset), and improve sealing performance .
A spherical mechanical sealing device is composed of a stator ring, stator ring seat, rotary ring, rotary ring seat, spring component and other parts, as shown in Fig. (1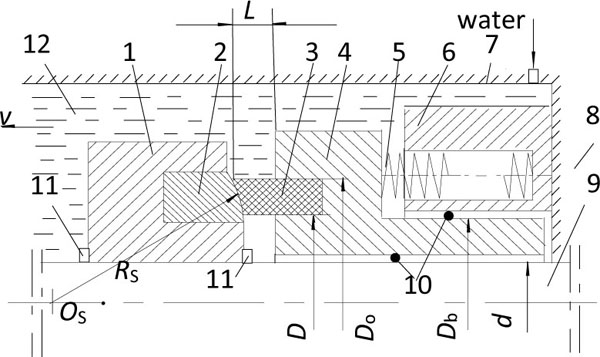 ).
).
Spherical mechanical sealing rings are shown in Fig. (2 ). The rotary ring material is bronze embedded in the rotary ring seat which is fixed on the stern shaft with both key and snap ring, and rotates along with the shaft; the stator ring is made of high polymer material (such as Feroform T12) instead of frequently-used carbon graphite which is very brittle, and easy to cause the corrosion of stainless steel and at last result in both leakage and failure of seal. The stator ring is fixed on the stator ring seat which can move along axial direction. The contact surfaces between both stator and rotary rings are spherical ones which play the role of both sealing and self-aligning functions.
). The rotary ring material is bronze embedded in the rotary ring seat which is fixed on the stern shaft with both key and snap ring, and rotates along with the shaft; the stator ring is made of high polymer material (such as Feroform T12) instead of frequently-used carbon graphite which is very brittle, and easy to cause the corrosion of stainless steel and at last result in both leakage and failure of seal. The stator ring is fixed on the stator ring seat which can move along axial direction. The contact surfaces between both stator and rotary rings are spherical ones which play the role of both sealing and self-aligning functions.
 |
Fig. (2) Spherical mechanical sealing rings: (a) stator ring (Feroform T12) (b) rotary ring. |
The only difference between both plane and spherical mechanical seals is their sealing surface shape. The former is flat surface, the latter is spherical surface (Fig. 2 ).
).
In two kinds of mechanical seals, there are some key parameters. Two important external force parameters including spring force and sealed medium pressure can make the spherical surface of stator ring keep in match-up with one of rotary ring all the while. The spring pressure value is necessary to ensure excellent sealing property when vessels navigate on the water. The pressure of the sealed medium outside of the spherical seal rings such as seawater can affect both contact pressure and temperature of the sealing surface severely, and the pressure of air inside of the rings is relative atmosphere pressure. Other dimensional parameters as following list can influence both contact pressure and temperature of sealing surfaces, too.
Taking the spherical mechanical seal on a certain marine stern shaft (in Fig. 1 ) as an example to discuss both sealing properties and its influence factors of spherical mechanical seal. Supposing stern shaft diameter d = 185 mm; the distance between static ring and rotary ring seats L= 8 ~12 mm (specified wear value is L= 8 mm); slip diameter Db = 208 mm; spring mean pressure is 0.2 MPa; sealing spherical radius of stator and rotary rings RS = 600 ~1200 mm; inner diameter of stator ring D = 201~204 mm; outer diameter of stator ring Do = 217 ~219 mm; the width of spherical sealing surface of stator and rotary rings is expressed with RS, D and Do. The ranges of parameters selected such as Db, D, Do, RS are considered according to the width of spherical sealing surface ((Do-D)/4), contact pressure and area ratio (namely, effective area of fluid pressure /nominal area of sealing surface) [15Y.Q. Gu, Practical Technology of Mechanical Seal., China Machine Press: Beijing, China, 2001.].
) as an example to discuss both sealing properties and its influence factors of spherical mechanical seal. Supposing stern shaft diameter d = 185 mm; the distance between static ring and rotary ring seats L= 8 ~12 mm (specified wear value is L= 8 mm); slip diameter Db = 208 mm; spring mean pressure is 0.2 MPa; sealing spherical radius of stator and rotary rings RS = 600 ~1200 mm; inner diameter of stator ring D = 201~204 mm; outer diameter of stator ring Do = 217 ~219 mm; the width of spherical sealing surface of stator and rotary rings is expressed with RS, D and Do. The ranges of parameters selected such as Db, D, Do, RS are considered according to the width of spherical sealing surface ((Do-D)/4), contact pressure and area ratio (namely, effective area of fluid pressure /nominal area of sealing surface) [15Y.Q. Gu, Practical Technology of Mechanical Seal., China Machine Press: Beijing, China, 2001.].
The list of the material parameters of each component of the spherical mechanical seal device is shown in Table 1.
In Table 1, the friction coefficient of among the parameters is from literature [15Y.Q. Gu, Practical Technology of Mechanical Seal., China Machine Press: Beijing, China, 2001.], and other physical parameters of materials of stator, rotary ring and their seats are from literature [16The Chinese Mechanical Engineering Society, The Chinese Mechanical Design., vol. 2. Jiangxi Science and Technology Publishing House: Nanchang, China, 2002.].
3. THERMAL-STRUCTURE COUPLING MODEL OF SPHERICAL MECHANICAL SEAL
Integral contact coupling method is used to solve thermal-structure problems of both stator and rotary rings. When the finite element model of both rings and their seats is established (unit: N-m-s), the boundary conditions to be difficultly determined is converted into the internal boundary ones, and the contact unit of the sealing surface is introduced to realize the connection between stator and rotary rings in order to ensure the temperatures of both contact surfaces of rings is the same.
Spherical mechanical seal ring model is the axial symmetry. Assume that spring force and external seawater pressure are as uniform pressures, and the water film reaction force between spherical sealing surfaces is linear distribution along the radial direction of the sealing surfaces. The cooling of the sealing rings is dealt with convection heat transfer boundary, and the friction heat between spherical surfaces is treated with by heat flux density boundary.
3.1. Building of Thermal-structure Coupling Model
The thermal-structure coupling model of spherical mechanical seal is established with ANSYS software. The heat structure coupling unit (PLANE13) of the spherical friction pair and material properties of the components is defined, the parameters of the material properties include elastic modulus, Poisson's ratio, and thermal expansion and thermal conductivity coefficients. Because the boundary conditions of the fitting parts of stator ring and its seat, rotary ring and its seat are difficult to determine, so both stator ring-seat and rotary ring-seat are integrated modeling, respectively, which will make the boundary conditions difficult to determine into the internal boundary. By using the contact wizard, the contact pair between spherical sealing surfaces of both stator and rotary rings is defined to realize the connections between two rings and to determine the contact area, contact pressure and temperature distributions of the two rings.
Both stator and rotary rings are bonded with own seat and divided grids, respectively. The spherical sealing surface of stator ring is defined as the contact unit and one of rotary ring as the object unit. Friction coefficient is filled in Friction Coefficient option, and a large number (usually over 108) in the Thermal Contact Conductance option to realize the automatic distribution of heat flux density and ensure that the corresponding node temperature of spherical sealing surfaces of both rings is basically consistent. Unsymmetry is input in the Stiffness Matrix option.
In order to improve the solution accuracy of the contact unit, the element size of the spherical sealing surfaces and sections of both stator and rotary rings is 0.5 mm, and one of the other portions of both rings is 1mm. The model consists of 3069 elements, 3191 nodes, as shown in Fig. (3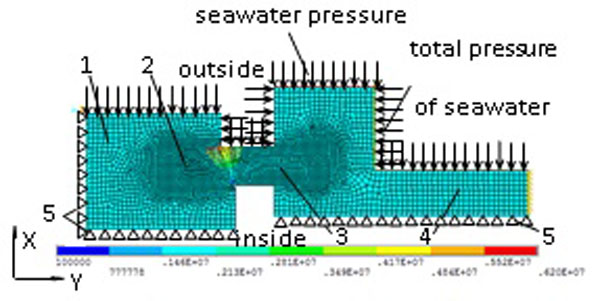 ).
).
It can be seen in Fig. (3 ), that the mean pressure ps of the spring is 0.2 MPa, and seawater pressure is decided on the basis of working condition of the spherical mechanical seal such as different water depth pressure (such as 6MPa), and relative atmosphere pressure pa is 0 MPa.
), that the mean pressure ps of the spring is 0.2 MPa, and seawater pressure is decided on the basis of working condition of the spherical mechanical seal such as different water depth pressure (such as 6MPa), and relative atmosphere pressure pa is 0 MPa.
3.2. Calculation of Convective Heat Transfer Coefficient
The convective heat transfer coefficient hm of sealing rings is calculated according following formulas
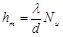
where, 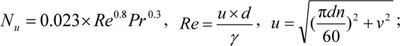 n is the shaft rotary speed, r·min-1; v is fluid axial velocity, m/s; u for the synthesis fluid speed at the outside of rotary ring seat, m/s; d is inner or outer diameter of sealing rings, m; γ is the kinematic viscosity of the fluid; λ is thermal conductivity of fluid, W/ (m.K); Re is the Reynolds number; Pr is the Planck number, J·s; Nu is Nusselt number.
n is the shaft rotary speed, r·min-1; v is fluid axial velocity, m/s; u for the synthesis fluid speed at the outside of rotary ring seat, m/s; d is inner or outer diameter of sealing rings, m; γ is the kinematic viscosity of the fluid; λ is thermal conductivity of fluid, W/ (m.K); Re is the Reynolds number; Pr is the Planck number, J·s; Nu is Nusselt number.
Assuming shaft speed n =300 r·min-1, fluid axial velocity v =1.0 m/s, and other physical parameters such as air and sea water at temperature T= 25°C are listed in Table 2. In Table 2 the parameters such as kinematic viscosity γ, thermal conductivity λ and Planck number Pr are from literature [17X.B. Zhao, Fluid Mechanics with Engineering Applications., Publishing House of Southeast University: Nanjing, 2012.].
3.3. Boundary Constraints
Displacement constraint boundary condition is shown in Fig. (3 ), the horizontal direction is the Y; the vertical direction is the X; and the U is constraint representation. At the left end of rotary ring seat is applied with axial constraint U(Y); the mounting position between stator ring seat and stern shaft and one between rotary ring seat and stern shaft are applied with vertical displacement constraint U(X); but the axial displacement of the stator ring seat isn’t be limited. Constant temperature 25°C is applied on the parts of both stator and rotary ring seats contacted with air or seawater respectively.
), the horizontal direction is the Y; the vertical direction is the X; and the U is constraint representation. At the left end of rotary ring seat is applied with axial constraint U(Y); the mounting position between stator ring seat and stern shaft and one between rotary ring seat and stern shaft are applied with vertical displacement constraint U(X); but the axial displacement of the stator ring seat isn’t be limited. Constant temperature 25°C is applied on the parts of both stator and rotary ring seats contacted with air or seawater respectively.
Because the contact pressure of spherical sealing surfaces is a nonlinear function versus heat flux density and sealing width, which can be applied on the surfaces with node function in ANSYS finite element software. As shown in Fig. (3 ), a linearly distributing seawater pressure is applied on the spherical sealing surfaces (i.e. water film force) of both stator and rotary rings. Supposing the air pressure inside the spherical sealing surface of both rings is 0, seawater pressure outside one is 6 MPa; uniform synthesis pressure which is equal to spring pressure plus seawater pressure is added on the spring acting surface of the stator ring seat, other positions marked arrows in Fig. (3
), a linearly distributing seawater pressure is applied on the spherical sealing surfaces (i.e. water film force) of both stator and rotary rings. Supposing the air pressure inside the spherical sealing surface of both rings is 0, seawater pressure outside one is 6 MPa; uniform synthesis pressure which is equal to spring pressure plus seawater pressure is added on the spring acting surface of the stator ring seat, other positions marked arrows in Fig. (3 ) are applied with seawater pressure.
) are applied with seawater pressure.
 |
Fig. (3) Boundary condition of pressure load 1- rotary seat; 2-rotary ring; 3- stator ring; 4- stator seat; 5- restriction U. |
The calculating formula of heat flux density of sealing rings is as following:
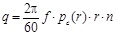
where q is heat flux density, W/m2; f is friction coefficient, f = 0.05; pc(r) is contact pressure between the spherical sealing surfaces, Pa; r is sealing ring mean radius (X direction, r = (D+D 0)/4), m; n is ring rotation speed.
The calculation of heat flux density of sealing rings involves the selection of friction coefficient f. Assume the spherical mechanical seal is in boundary or mix lubricating status at starting or stopping stage. Because Feroform T12 material of the stator ring is of excellent self-lubricating property and can commendably match with the bronze material of the rotary ring, so friction coefficient of sealing rings (f = 0.05) is selected [15Y.Q. Gu, Practical Technology of Mechanical Seal., China Machine Press: Beijing, China, 2001.].
According to the different fluid mediums, the convective heat transfer boundary is divided into two parts, in which one is the air convective heat transfer boundary inside sealing rings, and the other is seawater one outside ones as shown in Fig. (4 ). In order to facilitate the finite element analysis of the spherical mechanical seal, the arc length of spherical sealing surfaces is equally divided into 19 nodes. Node 1 is in the inside of the spherical sealing surface, and node 19 in the outside of one.
). In order to facilitate the finite element analysis of the spherical mechanical seal, the arc length of spherical sealing surfaces is equally divided into 19 nodes. Node 1 is in the inside of the spherical sealing surface, and node 19 in the outside of one.
 |
Fig. (4) Boundary condition of convection heat exchange. |
4. INFLUENCE OF STRUCTURE SIZE ON SEALING PROPERTIES
The structure sizes of the spherical mechanical seal, such as spherical radius, both inner and outer diameters of stator ring, and distance between stator and rotary ring seats, will severely influence sealing properties which include temperature, contact pressure and deformation of sealing rings.
Under working conditions unchanged, the influencing levels of the structure sizes are discussed respectively as following. The initial value of the key parameters applied in simulating calculation are RS = 600 mm,D=202 mm, D 0=218 mm, L= 8 mm; shaft speed n =300 r·min-1, seawater pressure pw= 6 MPa, mean pressure of the spring ps= 0.2 MPa, relative atmosphere pressure pa= 0 MPa.
4.1. Effect of Spherical Radius
Assuming spherical radius RS = 600~1200 mm, both the highest temperature and contact pressure versus spherical radius are shown in Figs. (5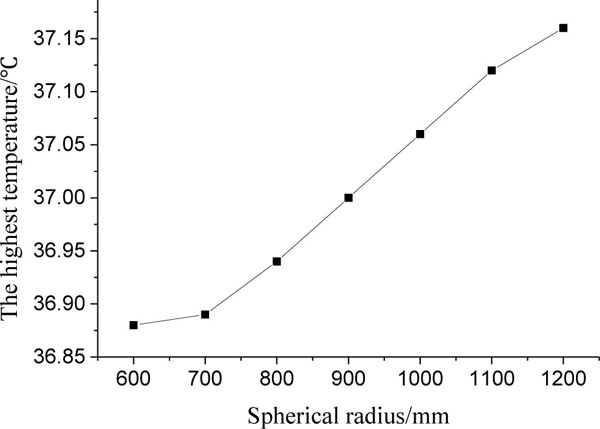 and 6
and 6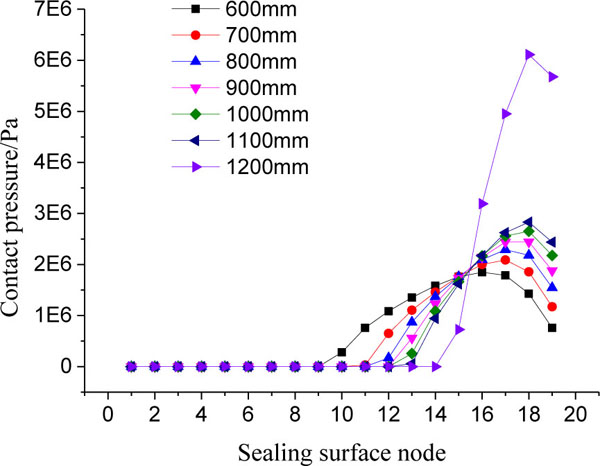 ), separately.
), separately.
 |
Fig. (5) The highest temperature versus spherical radius. |
 |
Fig. (6) Contact pressure versus sealing surface node. |
It can be seen in Fig. (5 ), that as the spherical radius increases from 600 mm to 1200 mm, the highest temperature of the spherical mechanical seal goes up by 0.28 °C. It can be explained that with the spherical radius increases, sealing area is expanded so that heat dissipation effect is poor. Simultaneously, due to the increase of spherical radius, the curvature of spherical sealing surface is decreased so that the contact area between stator ring and rotary ring is reduced and maximum contact pressure is raised, as shown in Fig. (6
), that as the spherical radius increases from 600 mm to 1200 mm, the highest temperature of the spherical mechanical seal goes up by 0.28 °C. It can be explained that with the spherical radius increases, sealing area is expanded so that heat dissipation effect is poor. Simultaneously, due to the increase of spherical radius, the curvature of spherical sealing surface is decreased so that the contact area between stator ring and rotary ring is reduced and maximum contact pressure is raised, as shown in Fig. (6 ). It can be seen in Fig. (6
). It can be seen in Fig. (6 ), that in opening region non contact node number is less than 9 nodes (taken 47% normal sealing area), the spherical sealing surfaces of both rings do not contact (namely, there is a gap in local region of sealing surfaces) and the contact pressure is 0, but the contact pressure in contact region (namely, contact pressure > 0) demonstrates parabolic variation distribution state. When the spherical radius is 1200 mm, maximum contact pressure is enhanced by 6MPa. It indicates that the contact pressure near the outside of the sealing surface is mutated under the combined action of both mechanical force and heating power.
), that in opening region non contact node number is less than 9 nodes (taken 47% normal sealing area), the spherical sealing surfaces of both rings do not contact (namely, there is a gap in local region of sealing surfaces) and the contact pressure is 0, but the contact pressure in contact region (namely, contact pressure > 0) demonstrates parabolic variation distribution state. When the spherical radius is 1200 mm, maximum contact pressure is enhanced by 6MPa. It indicates that the contact pressure near the outside of the sealing surface is mutated under the combined action of both mechanical force and heating power.
Take spherical radius 800 mm as an instance, the distribution states of temperature, contact pressure, both axial and radial deformations of its spherical sealing surface are shown in Fig. (7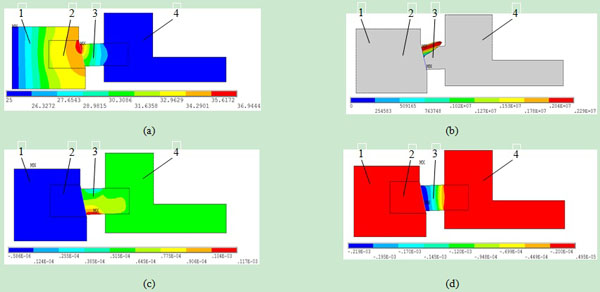 ). Under combined action of both external and thermal loads, both the highest temperature and maximum contact pressure of the spherical sealing surface appear outside of the sealing rings where the temperature rises sharply up to 36.9°C and maximum contact pressure is 2.29 MPa, as shown in Fig. (7a
). Under combined action of both external and thermal loads, both the highest temperature and maximum contact pressure of the spherical sealing surface appear outside of the sealing rings where the temperature rises sharply up to 36.9°C and maximum contact pressure is 2.29 MPa, as shown in Fig. (7a , b
, b ). Fig. (7a
). Fig. (7a ) shows that in the contact region the temperature of both stator and rotary rings is the same basically, but in the opening region the node temperature of the stator ring is lower than one of the rotary ring, their maximum temperature difference is 8°C. The closer to the inside of the sealing rings the region is, the more obvious this phenomenon. It is explained that the thermal conductivity of stator ring is significantly lower than that of the rotary one.
) shows that in the contact region the temperature of both stator and rotary rings is the same basically, but in the opening region the node temperature of the stator ring is lower than one of the rotary ring, their maximum temperature difference is 8°C. The closer to the inside of the sealing rings the region is, the more obvious this phenomenon. It is explained that the thermal conductivity of stator ring is significantly lower than that of the rotary one.
In Fig. (7c , d
, d ) both maximum axial and radial deformations of stator ring are 0.117 mm, 0.219 mm separately, and ones of rotary ring are 0.6 μm, 4.9 μm respectively. It indicates that the corresponding node deformations of the spherical sealing surfaces of both stator and rotary rings are not equal; the former is larger than the latter. The main cause is that both coefficient of thermal conductivity and elastic modulus of the rotary ring are higher than the stator ring.
) both maximum axial and radial deformations of stator ring are 0.117 mm, 0.219 mm separately, and ones of rotary ring are 0.6 μm, 4.9 μm respectively. It indicates that the corresponding node deformations of the spherical sealing surfaces of both stator and rotary rings are not equal; the former is larger than the latter. The main cause is that both coefficient of thermal conductivity and elastic modulus of the rotary ring are higher than the stator ring.
It shows that spherical radius has to be less than 1100 mm, 600mm is better in terms of structure size.
4.2. Inner Diameter of Stator Ring
When inner diameters D of the stator ring are 201~204 mm, both the highest temperature and contact pressure of sealing surface are shown in Figs. (8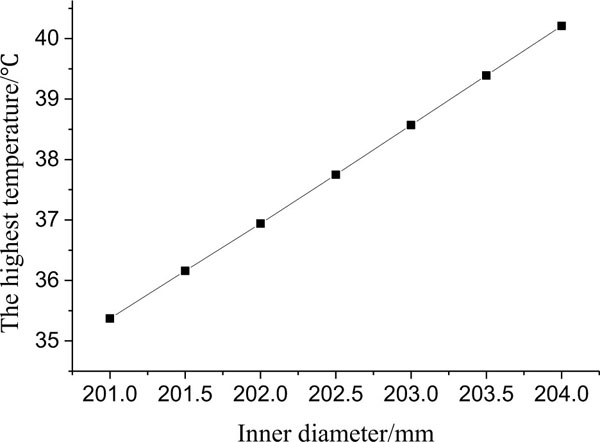 and 9
and 9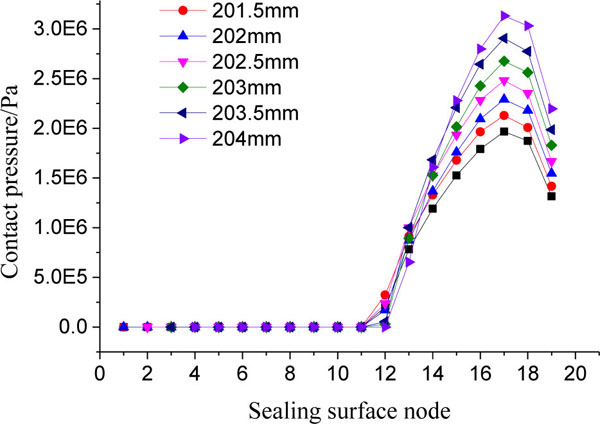 ), respectively.
), respectively.
 |
Fig. (8) The highest temperature versus inner diameter. |
 |
Fig. (9) Contact pressure versus sealing surface node. |
Fig. (8 ) shows that with the inner diameter increase of stator ring, the sealing width is reduced and the contact pressure is raised so that the highest temperature of spherical mechanical seal is increased linearly, its variation amplitude is 4.9°C. Fig. (9
) shows that with the inner diameter increase of stator ring, the sealing width is reduced and the contact pressure is raised so that the highest temperature of spherical mechanical seal is increased linearly, its variation amplitude is 4.9°C. Fig. (9 ) demonstrates that non contact node number in difference D is almost the same (11 or 12 nodes), and the variation amplitude of the contact pressure is 1.2 MPa. The reason is that though the contact pressure is raised with the sealing width reduction, the thermal dissipation condition of the sealing surface is improved so that the contact pressure resulted from heating power is significantly declined, and the highest contact pressure is decreased, too.
) demonstrates that non contact node number in difference D is almost the same (11 or 12 nodes), and the variation amplitude of the contact pressure is 1.2 MPa. The reason is that though the contact pressure is raised with the sealing width reduction, the thermal dissipation condition of the sealing surface is improved so that the contact pressure resulted from heating power is significantly declined, and the highest contact pressure is decreased, too.
Thus it can be seen that outer diameter of stator ring is as small as possible under specified shaft diameter.
4.3. Outer Diameter of Stator Ring
In the case of working conditions unchanged, the influence of outer diameter of the stator ring (Do= 217~219 mm) on the sealing properties of spherical mechanical seal is analyzed, both the highest temperature and contact pressure of sealing surface are shown in Figs. (10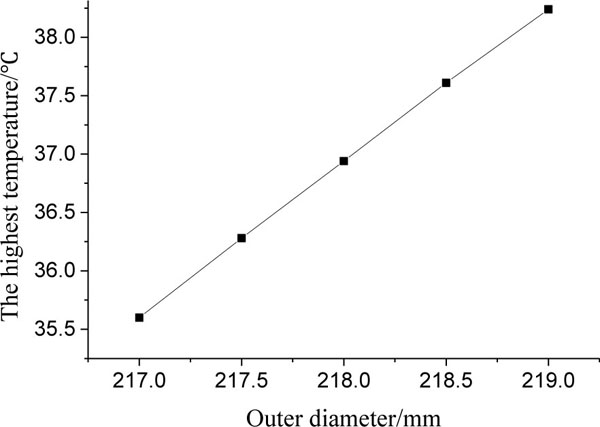 and 11
and 11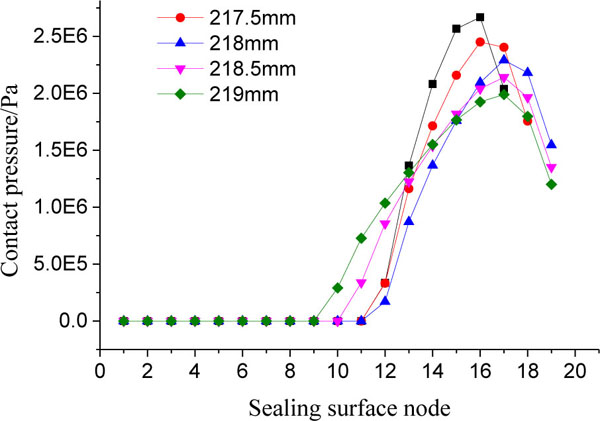 ), separately.
), separately.
Figs. (10 and 11
and 11 ) show that with the increase of the outer diameter of the stator ring, the sealing width of both stator and rotary rings is increased, the contact pressure of sealing surface is decreased and the node position of maximum contact pressure is shifted toward the outside of sealing surface due to contact area increase (namely, growing in contact node quantity), but thermal dissipation property of the spherical mechanical seal is declined, finally the highest temperature are raised linearly, whose variation amplitude is 2.7°C. In Fig. (11
) show that with the increase of the outer diameter of the stator ring, the sealing width of both stator and rotary rings is increased, the contact pressure of sealing surface is decreased and the node position of maximum contact pressure is shifted toward the outside of sealing surface due to contact area increase (namely, growing in contact node quantity), but thermal dissipation property of the spherical mechanical seal is declined, finally the highest temperature are raised linearly, whose variation amplitude is 2.7°C. In Fig. (11 ), non contact node number in difference Do is 9~12, and the contact pressure is distributed on 9~19 node, whose variation trend is identical as one in Fig. (9
), non contact node number in difference Do is 9~12, and the contact pressure is distributed on 9~19 node, whose variation trend is identical as one in Fig. (9 ), but the maximum contact pressure (variation amplitude is 0.7 MPa) is lower than one in Fig. (9
), but the maximum contact pressure (variation amplitude is 0.7 MPa) is lower than one in Fig. (9 ). It can be seen in Figs. (9
). It can be seen in Figs. (9 and 11
and 11 ), that contact pressure of sealing surface is clearly affected with structure size of the stator ring, namely, the influence of outer or inner diameter increase on the contact pressure are on the contrary. Therefore, both the highest temperature and contact pressure shall be jointly considered to select the outer diameter of stator ring that is about 218 mm suitably.
), that contact pressure of sealing surface is clearly affected with structure size of the stator ring, namely, the influence of outer or inner diameter increase on the contact pressure are on the contrary. Therefore, both the highest temperature and contact pressure shall be jointly considered to select the outer diameter of stator ring that is about 218 mm suitably.
 |
Fig. (10) The highest temperature versus outer diameter. |
 |
Fig. (11) Contact pressure versus sealing surface node. |
4.4. Distance Between Both Ring Seats
The distance L between stator and rotary ring seats can influence spherical sealing properties. Assuming the distance is from 8 mm to 12 mm, the highest corresponding temperature and contact pressure of the spherical sealing surface are shown in Figs. (12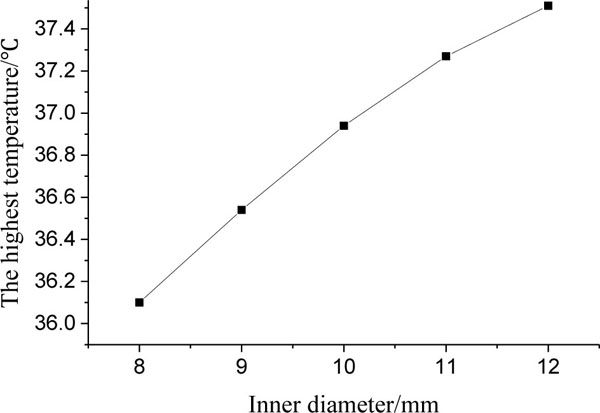 and 13
and 13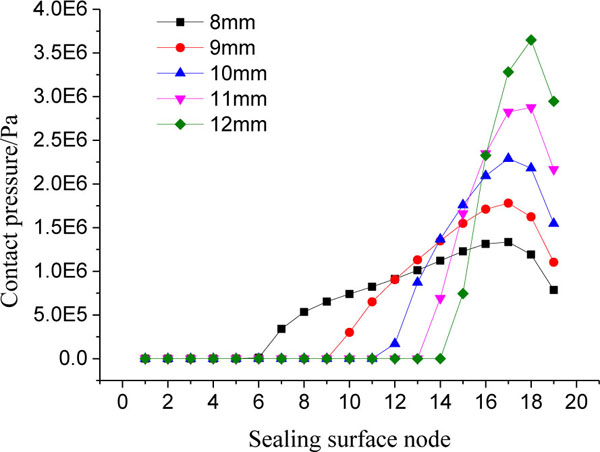 ), respectively. The axial deformation of both stator and rotary rings versus distance L is shown in Fig. (14
), respectively. The axial deformation of both stator and rotary rings versus distance L is shown in Fig. (14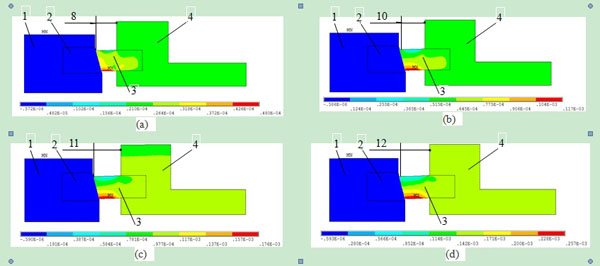 ).
).
 |
Fig. (12) The highest temperature versus distance of two rings. |
 |
Fig. (13) Contact pressure versus sealing surface node. |
As the distance between two ring seats is increased from 8 mm to12 mm, both axial length and deformation of the stator ring are increased, and both ring stiffness and contact area of sealing surface are decreased. For an instance, when distance L is 8 mm and 12 mm, the non contacted node numbers of the sealing rings are 6 and 14 node separately, it means that the longer the L is, more severe the deformation of the stator ring and the higher the contact pressure of the sealing surface. Finally, the highest temperature of spherical mechanical seal is raised from 36.1°C to 37.5°C, as shown in Fig. (12 ); maximum contact pressure is increased from 1.26 MPa to 3.62 MPa, as shown in Fig. (13
); maximum contact pressure is increased from 1.26 MPa to 3.62 MPa, as shown in Fig. (13 ). Under different distance (L= 8, 10, 11, 12 mm), the maximum axial deformations of stator ring as shown in Fig. (14a
). Under different distance (L= 8, 10, 11, 12 mm), the maximum axial deformations of stator ring as shown in Fig. (14a -d
-d ), are 0.048, 0.117, 0.176, 0.257 mm separately. The analysis indicates that the distance between stator and rotary ring seats can influence on contact pressure of sealing surface obviously so that the distance shall be decreased as far as possible under specified wear value.
), are 0.048, 0.117, 0.176, 0.257 mm separately. The analysis indicates that the distance between stator and rotary ring seats can influence on contact pressure of sealing surface obviously so that the distance shall be decreased as far as possible under specified wear value.
5. TEMPERATURE TEST OF SPHERICAL SEALING SURFACE
The test installation of spherical mechanical seal is shown as Fig. (15 ). 3 temperature sensors are assembled on different radius of the spherical sealing surface of the stator ring respectively, and their distance from sealing surface is 2mm. and other sensors (such as fluid pressure sensors and so on) are fixed on the same sealing surface, shown as Fig. (16
). 3 temperature sensors are assembled on different radius of the spherical sealing surface of the stator ring respectively, and their distance from sealing surface is 2mm. and other sensors (such as fluid pressure sensors and so on) are fixed on the same sealing surface, shown as Fig. (16 ).
).
 |
Fig. (15) Test installation of spherical mechanical seal. |
 |
Fig. (16) Temperature sensor arrangement. |
The temperature test of the spherical sealing surface is processed under the conditions: D=202 mm, D0=218 mm, RS=600mm, spring pressure ps = 0.2MPa, water pressure pw = 6 MPa, n= 300 r/min. Test results are shown in Table 3.
Test results shows that the highest temperature of the spherical sealing surface in theoretical calculation (as shown in Fig. (10 ) is lower 9.8% than the average value of one in test, which indicates theoretical calculation value is preferably consistent with test results, and states thermal-structure coupling model of spherical mechanical seal is relatively reasonable. But the contact pressure test problem of sealing surface has to be remained to research in future because of the test difficulty.
) is lower 9.8% than the average value of one in test, which indicates theoretical calculation value is preferably consistent with test results, and states thermal-structure coupling model of spherical mechanical seal is relatively reasonable. But the contact pressure test problem of sealing surface has to be remained to research in future because of the test difficulty.
CONCLUSION
The thermal-structure coupling model of the spherical mechanical seal of a marine stern shaft (d =185 mm) was established with ANSYS finite element method, the distribution rules of temperature, contact pressure and deformation of the spherical sealing surface were studied under different structure size conditions, and following conclusions were obtained:
- With the increase of spherical radius, both the highest temperature and maximum contact pressure are raised, and the contact region of spherical sealing surfaces is decreased, and the contact pressure demonstrates parabolic variation distribution state in contacting region and maximum contact pressure is enhanced by 6 MPa, while opening region is expanded more than 9 nodes, taken about 47% of normal sealing area. Therefore, spherical radius RS= 600mm is better.
- As inner or outer diameter of stator ring is increased, the width of sealing surface is decreased or augmented, and the highest temperatures of two kinds of diameters are all enhanced linearly, but the variation amplitude of both maximum contact pressure and temperature of the former are 1.2 MPa and 4.9 °C, ones of the latter 0.7 MPa and 2.7 °C, respectively, the highest contact pressure occurs near the outside of the sealing surface. It indicates that the width of sealing surface have important influence on both contact pressure and temperature of the sealing surface, and both inner and outer diameters of the stator ring are proposed 202 mm and 218mm.
- With the increase of the distance between stator and rotary rings, both highest temperature and maximum contact pressure of sealing surface are raised so that the distance shall be decreased to specified wear value (8mm) as far as possible.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was financially supported by the project of Natural Science Foundation of China (No.51379168), Key Natural Science Foundation of China (No.51139005).
REFERENCES
| [1] | Z.G. Zhang, S.W. Yao, and X.H. Zhou, "Research on mechanical deformation of friction pair of stern shaft sealing device in submarine under great depth", Ocean Eng., no. 6, pp. 12-14, 2004. |
| [2] | A.P. Nyemeck, N. Brunetière, and B. Tournerie, "A multiscale approach to the mixed lubrication regime: application to mechanical seals", Tribol. Lett., vol. 47, pp. 417-429, 2012. [http://dx.doi.org/10.1007/s11249-012-9997-5] |
| [3] | A.P. Nyemeck, N. Brunetière, and B. Tournerie, "Parametric study of the behavior of a mechanical face seal operating in mixed and TEHD lubrication regimes", In: Proceedings of the ASME 11th Biennial Conference on Engineering Systems Design and Analysis, ESDA2012, Nantes, France, 2012. [http://dx.doi.org/10.1115/ESDA2012-82743] |
| [4] | C. Minet, N. Brunetière, and B. Tournerie, "A deterministic mixed lubrication model or mechanical seals", J. Tribol., vol. 133, no. 4, p. 042203, 2011. [http://dx.doi.org/10.1115/1.4005068] |
| [5] | R.L. Phillips, L.E. Jacobs, and P. Merati, "Experimental determination of the thermal characteristics of a mechanical seal and its operating environment", Tribol. T., vol. 40, pp. 559-568, 1997. [http://dx.doi.org/10.1080/10402009708983693] |
| [6] | M.D. Pascovici, and I. Etsion, "A thermo-hydrodynamic analysis of a mechanical face seal", J. Tribol., vol. 114, pp. 639-645, 1992. [http://dx.doi.org/10.1115/1.2920930] |
| [7] | W. Liu, Y. Liu, and J.J. Zhai, "Three-dimensional flow–heat coupling model of a wavy-tilt-dam mechanical seal", Tribol. Trans., vol. 56, no. 6, pp. 1146-1155, 2013. [http://dx.doi.org/10.1080/10402004.2013.812758] |
| [8] | I. Etsion, Y. Kligerman, and G. Halperin, "Analytical and experimental investigation of laser-textured mechanical seal faces", Tribol. Trans., vol. 42, no. 3, pp. 511-516, 1999. [http://dx.doi.org/10.1080/10402009908982248] |
| [9] | I. Etsion, and G. Halperin, "A laser surface textured hydrostatic mechanical seal", Tribol. Trans., vol. 45, no. 3, pp. 430-434, 2002. [http://dx.doi.org/10.1080/10402000208982570] |
| [10] | M. Pustan, O. Belcin, and C. Birleanu, "Mechanical seals with oscillating stator", Meccanica, vol. 48, pp. 1191-1200, 2013. [http://dx.doi.org/10.1007/s11012-012-9660-0] |
| [11] | R.F. Salant, and B. Cao, "Unsteady analysis of a mechanical seal using Duhamel’s method", J. Tribol., vol. 127, no. 3, pp. 623-631, 2005. [http://dx.doi.org/10.1115/1.1924427] |
| [12] | X.D. Peng, W. Liu, and S.X. Bai, "Effects analysis of thermo-elastic deformation on the performance of hydrostatic mechanical seals in reactor coolant pumps", J. Mechl. Eng., vol. 46, no. 23, pp. 146-153, 2010. [http://dx.doi.org/10.3901/JME.2010.23.146] |
| [13] | B. Qin, Z.L. Liu, and X.H. Zhou, "Research on influence of dam seal structure on performance of marine mechanical seal", In: Improving Multimodal Transportation Systems - Information, Safety, and Integration - Proceedings of the 2nd International Conference on Transportation Information and Safety, ACS: United States. 2013, pp. 2259-2264. [http://dx.doi.org/10.1061/9780784413036.303] |
| [14] | X.M. Zhu, "Research on Numerical Analysis and Optimization of Mechanical Sealing Performance", M.s. thesis, Wuhan University of Technology, Wuhan, China, 2005. |
| [15] | Y.Q. Gu, Practical Technology of Mechanical Seal., China Machine Press: Beijing, China, 2001. |
| [16] | The Chinese Mechanical Engineering Society, The Chinese Mechanical Design., vol. 2. Jiangxi Science and Technology Publishing House: Nanchang, China, 2002. |
| [17] | X.B. Zhao, Fluid Mechanics with Engineering Applications., Publishing House of Southeast University: Nanjing, 2012. |









