- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mechanical Engineering Journal
(Discontinued)
ISSN: 1874-155X ― Volume 14, 2020
Mode-decomposing Analysis of the Extreme Load in Hybrid Electric Vehicles Using Extreme Value Theory
Jian Zhou, Jixin Wang, Hongbin Chen*
Abstract
In a hybrid electric vehicle (HEV), the hybrid system, which is equipped with an engine and a motor, is a key component. However, given the multimode characteristics of HEV, the original extreme load of the engine or motor is not independent and the random variables cannot be directly fitted by the extreme value theory (EVT). Thus, this paper proposes a mode-decomposing application method (MDAM) using EVT. Based on the method, three typical distributions, including the Fréchet distribution, the Gumbel distribution, and the Weibull distribution, were combined as a unified expression, and it was adopted to fit the extreme loads within different modes of HEV. By comparing the fitting results, especially the shapes of the curves, the distributions of the load under different modes vary from each other, so the feasibility and necessity of MDAM in HEV are proved, and a new thought for fitting the extreme load in HEV is provided, which will contribute to improve the fitting accuracy.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 136
Last Page: 147
Publisher Id: TOMEJ-10-136
DOI: 10.2174/1874155X01610010136
Article History:
Received Date: 29/12/2015Revision Received Date: 02/06/2016
Acceptance Date: 08/06/2016
Electronic publication date: 21/07/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Correspondence: Address correspondence to this author at the Nanling Campus of Jilin University, No. 5988 of Renmin Avenue, Changchun, Jilin Province, China; Postcard: 130022; Tel: +86 13596157924; E-mail: jxwang@jlu.edu.cn
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 29-12-2015 |
Original Manuscript | Mode-decomposing Analysis of the Extreme Load in Hybrid Electric Vehicles Using Extreme Value Theory | |
1. INTRODUCTION
Damage in vehicle components is mainly caused by fatigue process, which are mainly influenced by extreme loads [1C.P. Przybyla, and D.L. Mcdowell, "Simulated microstructure-sensitive extreme value probabilities for high cycle fatigue of duplex Ti–6Al–4V", Int. J. Plast., vol. 27, pp. 1871-1895, 2011.
[http://dx.doi.org/10.1016/j.ijplas.2011.01.006] , 2J.X. Wang, N.X. Wang, Z.Y. Wang, Y.S. Zhang, and L. Liu, "Determination of the minimum sample size for the transmission load of a wheel loader based on multi-criteria decision-making technology", J. Terramechs., vol. 49, pp. 147-160, 2012.
[http://dx.doi.org/10.1016/j.jterra.2012.02.001] ]. Some related studies [3J. Petit, and C. Sarrazin-Baudoux, "Some critical aspects of low rate fatigue crack propagation in metallic materials", Int. J. Fatigue, vol. 32, pp. 962-970, 2010.
[http://dx.doi.org/10.1016/j.ijfatigue.2009.10.013] , 4T.A. Sawaguchi, G. Kausträter, A. Yawny, M. Wagner, and G. Eggeler, "Crack initiation and propagation in 50.9 at. pct Ni-Ti pseudoelastic shape-memory wires in bending-rotation fatigue", Metall. Mater. Trans., A Phys. Metall. Mater. Sci., vol. 34, pp. 2847-2860, 2003.
[http://dx.doi.org/10.1007/s11661-003-0186-x] ] show that extreme loads play a considerable role in the initiation and propagation of fatigue cracks, and final fatigue fractures are also caused by extreme loads. Therefore, a reasonable estimation of the extreme loads combined with their frequencies are the basis of research on the fatigue analysis and life prediction of the key components, and studies on extreme loads are significant and necessary. However, considering the limitations of economic conditions, technical level, development cycles and other external conditions in practical applications, obtaining the load time history of the vehicles in full-life time is difficult, even impossible. Only several typical road conditions can be selected for load sample measurement, which will result in the leakage of important extreme loads. Important issues are raised on the extraction of useful load information from limited load samples. Meanwhile, the application of a reliable method to reasonably estimate the occurrence probability and frequency of extreme loads in full-life time is important. A smart solution to this problem is the application of EVT.
EVT is a branch of statistics that deals with extreme values deviating from the mean of a probability distribution. This theory was first proposed by Fisher and Tippett [5A. Sawaguchi, G. Kausträter, A. Yawny, M. Wagner, and G. Eggeler, "Crack initiation and propagation in 50.9 at. pct Ni-Ti pseudoelastic shape-memory wires in bending-rotation fatigue", Tran. A, vol. vol. 34, 2003pp. 2847-2860
[http://dx.doi.org/10.1007/s11661-003-0186-x] ], and was formalized by Gnedenko [6B. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire", Ann. Math., vol. 44, pp. 423-453, 1943.
[http://dx.doi.org/10.2307/1968974] ] who showed that the distribution of the block-maxima of a sample of the independent and identically distributed random variables converges to a member of the extreme value distribution. EVT usually acts as a robust statistical model for understanding and forecasting events that occur with small probabilities but extreme impact. It has attracted an increasing interest in a large number of scientific fields and practical applications, such as structural safety [7A. Naess, O. Gaidai, and O. Batsevych, "Extreme value statistics of combined load effect processes", Struct. Saf., vol. 31, pp. 298-305, 2009.
[http://dx.doi.org/10.1016/j.strusafe.2008.09.004] -9M. Behzad, and M. Mohsen, "A spatio-temporal dynamic regression model for extreme wind speeds", Extremes, vol. 17, pp. 221-245, 2014.
[http://dx.doi.org/10.1007/s10687-014-0180-2] ], hydrology [10N. Chini, and P.K. Stansby, "Extreme values of coastal wave overtopping accounting for climate change and sea level rise", Coast. Eng., vol. 65, pp. 27-37, 2012.
[http://dx.doi.org/10.1016/j.coastaleng.2012.02.009] -12P. Willems, A. Guillou, and J. Beirlant, "Bias correction in hydrologic GPD based extreme value analysis by means of a slowly varying function", J. Hydrol. (Amst.), vol. 338, pp. 221-236, 2007.
[http://dx.doi.org/10.1016/j.jhydrol.2007.02.035] ], finance [13H. Sawsan, P. Ser-Huang, and T. Jonathan, "Portfolio risk assessment using multivariate extreme value methods", Extremes, vol. 17, pp. 531-556, 2014.
[http://dx.doi.org/10.1007/s10687-014-0194-9] -15A. K. Singh, D.E. Allen, and P.J. Robert, "Extreme market risk and extreme value theory", Math. Comput. Simulat., vol. 94, pp. 310-328, 2013.], meteorological and climate events [16R. Mínguez, M. Menéndez, F.J. Méndez, and I.J. Losada, "Sensitivity analysis of time-dependent generalized extreme value models for ocean climate variables", Adv. Water Resour., vol. 33, pp. 833-845, 2010.
[http://dx.doi.org/10.1016/j.advwatres.2010.05.003] -18C. Marty, and J. Blanchet, "Long-term changes in annual maximum snow depth and snowfall in Switzerland based on extreme value statistics", Clim. Change, vol. 111, pp. 705-721, 2012.
[http://dx.doi.org/10.1007/s10584-011-0159-9] ]. The seamless applicability of EVT in a large variety of fields can be attributed to its definition of an “extreme” in a universal manner instead of adopting the subjective definition of an “extreme” as a very large phenomenon [19V. Lucarini, D. Faranda, G. Turchetti, and S. Vaienti, "Extreme value theory for singular measures, Chaos: An interdisciplinary", J. Nonlinear Sci., vol. 22, pp. 1-16, 2012.].
The initial load samples of previous studies [20A. K. Singh, D.E. Allen, and P.J. Robert, "Extreme market risk and extreme value theory", Math. Comput. Simulat., vol. 94, pp. 310-328, 2013., 21M. Kasperski, and R. Hoxey, "Extreme-value analysis for observed peak pressures on the Silsoe cube", J. Wind Eng. Ind. Aerodyn., vol. 96, pp. 994-1002, 2008.
[http://dx.doi.org/10.1016/j.jweia.2007.06.024] ] on extreme load distribution are independent and identically distributed random variables, which can be fitted by EVT directly. However, considering the multimode operating characteristics of HEV, the load properties of each terminal (engine, motor and generator), which usually works under different conditions, have significant differences. Therefore, the load samples of HEV do not conform to the prerequisite of EVT and cannot be directly fitted using EVT [22J. Ekengren, and J. Bergström, "Extreme value distributions of inclusions in six steels", Extremes, vol. 15, pp. 257-265, 2012.
[http://dx.doi.org/10.1007/s10687-011-0139-5] ]. found that the extreme distribution of the size of non-metallic inclusions in different steels varies from each other. Examples of all three generalized extreme value (GEV, a typical approach of EVT) distribution modes are found for fatigue initiating inclusions in six different high performance steels with different grades and processing routes. Inspired by their research, the extreme load samples of HEV may also be fitted with different functions, and this paper focuses on the feasibility and necessity of this thought. In this paper, a new EVT application method, mode-decomposing application method, for short is MDAM, is proposed by combining the peculiar multimode operating characteristics of HEV. The main research flows are as follows. First, initial torque data are obtained using ADVISOR simulation. A variety of drive cycles are gathered to simulate the traffic information in real circumstances to improve the representation of the acquired sample data. Then, according to the working principle of HEV, the output speed and the torque of each terminal under different operating modes are selected and fitted using GEV. GEV distribution type (Fréchet distribution, Gumbel distribution or Weibull distribution) of each mode is determined. Finally, the necessity and feasibility of MDAM is verified.
2. MUTIPLE OPERATING MODES OF HEV
HEV is a type of hybrid vehicle that combines a conventional internal combustion engine (ICE) propulsion system with an electric propulsion system [23C. J. Orie, and Q. I. Nwatu, "Challenges of energy saving crisis as a panacea to hybrid electric vehicle (HEV)", Mediterranean J. Soc. Sci., vol. 2, November 2011.]. Modern HEVs take the advantage of high efficiency technologies such as regenerative braking, which converts kinetic energy into electric energy for battery charging. Some HEVs use the ICE to generate electricity by spinning the generator. This electricity is usually used to recharge batteries or to power the electric drive motors directly. Many HEVs reduce idle emissions by shutting down the ICE at idle and restarting the ICE when it is required, which is known as the start–stop system. According to the way in which power is supplied to the drivetrain, HEV can be classified into three types: the series type, the parallel type and the series–parallel type. In this study, a Prius series–parallel hybrid electric vehicle (SPHEV) is adopted as an example to introduce the working principle and typical operating modes of HEV.
The structure of a SPHEV hybrid system [24Toyota Motor Corporation, TOYOTA Hybrid System THS II, May 2003.] is shown in Fig. (1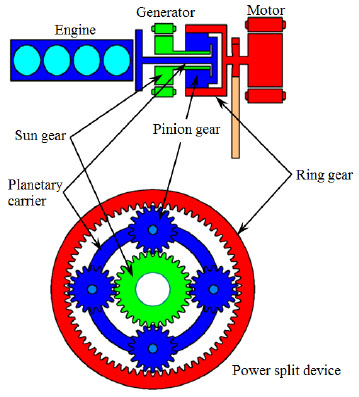 ), which is equipped with an engine and a motor. Both of the engine and the motor can simultaneously transmit the power to drive the wheels. In this system, another motor is used as a generator to charge the battery or as a starter to start the engine. To save energy, the engine, motor and generator are often operated comprehensively according to the driving conditions. The power split device is a planetary-gear-type powertrain that comprises a sun gear, a round planetary carrier, four pinion gears and a ring gear. The sun gear is linked to the generator, which can rotate clockwise and counter clockwise. Therefore, the sun gear also has two rotating forms. The planetary carrier is linked to the engine, which can rotate clockwise only. One end of the ring gear is linked to the motor and the other end is linked to the wheels. The motor can rotate both clockwise and counter clockwise, similar to the generator; thus, the ring gear also has two rotating forms. The clockwise and counter-clockwise rotation of the ring gear also means that the vehicle goes forward and backward. Therefore, the vehicle can drive in different operating modes by controlling the operating state of the three terminals. This paper extracts five representative [25A.K. Gupta, and C.P. Ramanarayanan, "Analysis of circulating power within hybrid electric vehicle transmissions", Mechanism Mach. Theory, vol. 64, pp. 131-143, 2013.
), which is equipped with an engine and a motor. Both of the engine and the motor can simultaneously transmit the power to drive the wheels. In this system, another motor is used as a generator to charge the battery or as a starter to start the engine. To save energy, the engine, motor and generator are often operated comprehensively according to the driving conditions. The power split device is a planetary-gear-type powertrain that comprises a sun gear, a round planetary carrier, four pinion gears and a ring gear. The sun gear is linked to the generator, which can rotate clockwise and counter clockwise. Therefore, the sun gear also has two rotating forms. The planetary carrier is linked to the engine, which can rotate clockwise only. One end of the ring gear is linked to the motor and the other end is linked to the wheels. The motor can rotate both clockwise and counter clockwise, similar to the generator; thus, the ring gear also has two rotating forms. The clockwise and counter-clockwise rotation of the ring gear also means that the vehicle goes forward and backward. Therefore, the vehicle can drive in different operating modes by controlling the operating state of the three terminals. This paper extracts five representative [25A.K. Gupta, and C.P. Ramanarayanan, "Analysis of circulating power within hybrid electric vehicle transmissions", Mechanism Mach. Theory, vol. 64, pp. 131-143, 2013.
[http://dx.doi.org/10.1016/j.mechmachtheory.2013.01.011] ] to analyze.
Motor-only mode (Fig. 2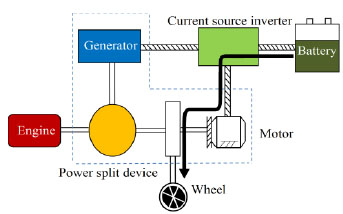 ): the engine is shut down when the vehicle is at a low speed and requires a small torque. And the motor, which is charged by the battery, drives the ring gear to rotate.
): the engine is shut down when the vehicle is at a low speed and requires a small torque. And the motor, which is charged by the battery, drives the ring gear to rotate.
Regenerative braking mode (Fig. 3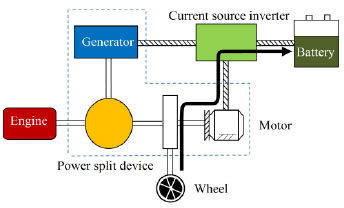 ): when the vehicle is decelerating, braking or going downhill, the engine is shut down. And the motor, driven by the wheels, is used as the generator. Therefore, this kind of braking energy is converted into electrical energy, which is then stored in the battery. This application is useful for city driving conditions with the frequent acceleration and deceleration.
): when the vehicle is decelerating, braking or going downhill, the engine is shut down. And the motor, driven by the wheels, is used as the generator. Therefore, this kind of braking energy is converted into electrical energy, which is then stored in the battery. This application is useful for city driving conditions with the frequent acceleration and deceleration.
 |
Fig. (1) Structure of SPHEV hybrid system. |
Combined power mode (Fig. 4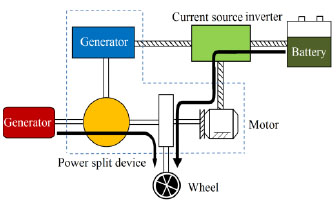 ): when the vehicle requires high power output such as during acceleration and climbing, the battery charges the
): when the vehicle requires high power output such as during acceleration and climbing, the battery charges the
motor to drive the vehicle together with the engine.
Engine-only mode (Fig. 5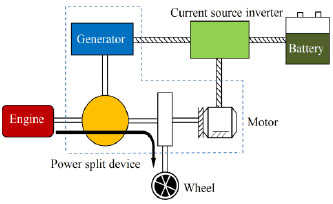 ): the engine drives the vehicle alone when the vehicle cruises. At this point, the generator spins reversely and provides a reversed torque that drives the vehicle forward.
): the engine drives the vehicle alone when the vehicle cruises. At this point, the generator spins reversely and provides a reversed torque that drives the vehicle forward.
Engine/charge mode (Fig. 6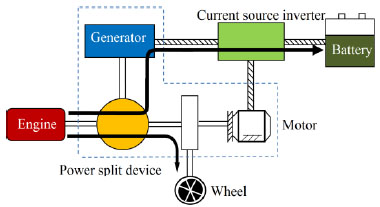 ): when the vehicle requires little power, part of the torque provided by the engine is used to drive the vehicle. The other part is used to drive the generator to generate energy, which is used to charge the battery.
): when the vehicle requires little power, part of the torque provided by the engine is used to drive the vehicle. The other part is used to drive the generator to generate energy, which is used to charge the battery.
Research on the operating principle and modes of SPHEV reveals that the vehicle changes frequently among different modes and that each terminal usually works in different conditions, thus resulting in different output speeds and torque characteristics [25A.K. Gupta, and C.P. Ramanarayanan, "Analysis of circulating power within hybrid electric vehicle transmissions", Mechanism Mach. Theory, vol. 64, pp. 131-143, 2013.
[http://dx.doi.org/10.1016/j.mechmachtheory.2013.01.011] ]. Therefore, the load distribution characteristics of each terminal in different operating modes are significantly different.
 |
Fig. (2) Motor-only mode. |
 |
Fig. (3) Regenerative braking mode. |
 |
Fig. (4) Combined power mode. |
 |
Fig. (5) Engine-only mode. |
 |
Fig. (6) Engine/charge mode. |
3. DATA ACQUISITION AND PROCESSING
3.1. Data Acquisition
This paper takes the Prius SPHEV as an example to analyze the extreme value distribution of the output torque of each terminal under different modes. The original data are obtained using ADVISOR simulation. To ensure the randomness of the sample data and acquire reliable road information, the vehicles are operated under a variety of speed conditions. Given the proportion of 17:28:55 for the road conditions of highways, city highways and rural highways, the following conditions are selected [26Z. Zou, D. Scott, B. Kevin, O'. Michael, H. Terry, R. Robert, W. Steve, and V. K. Sharma, "A new composite drive cycle for heavy-duty hybrid electric class 4-6 vehicles", SAE Trans., vol. 113, pp. 771-778, 2004.]: Highway Fuel Economy Test (HWFET), Urban Dynamometer Driving Schedule (UDDS), and a combination cycle (one Urban Drive Cycle – Extra Urban Drive Cycle (ECE_EUDC) and two Japan 10-15 (1015_6PRIUS) cycles). The speeds required under the four basic simulation conditions (HWFET, UDDS, ECE_EUDC and 1015_6PRIUS) are shown in Fig. (7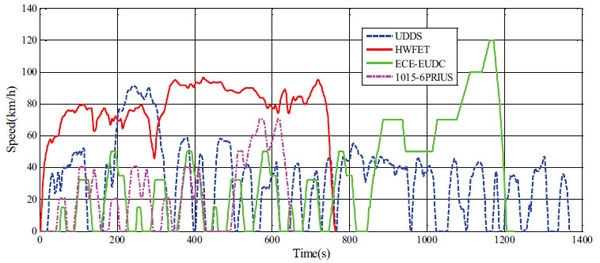 ).
).
 |
Fig. (7) Speed variation curves under different driving conditions. |
3.2. Data Processing of Each Mode
According to the working principle of SPHEV, the obtained original data must be screened and classified into different modes. The operating conditions of the engine, generator and motor differ from each other when working under different modes. Therefore, the load data of each mode can be screened and classified by comparing the positive and negative relationships of the output torque and rotational speed. Five representative operating modes are screened, and the proportion of each mode is calculated based on the working principle of the SPHEV and characteristics of the load (as shown in Table 1).
4. EXTREME LOAD DISTRIBUTION OF EACH TERMINAL UNDER DIFFERENT OPERATING MODES
4.1. Original Distribution of Each Terminal
The load distribution column diagrams (Fig. 8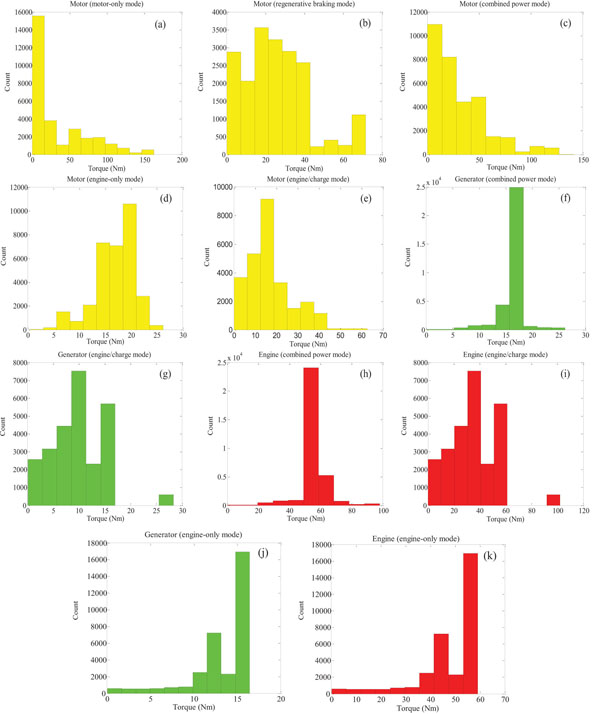 ) of each terminal under different operating modes are obtained through the preliminary statistical analysis of each load data group. EVT usually focuses on random variables with rare occurrence but significant influences [27L.L. Haan, and A. Ferreira, Extreme Value Theory., Springer, 2006.
) of each terminal under different operating modes are obtained through the preliminary statistical analysis of each load data group. EVT usually focuses on random variables with rare occurrence but significant influences [27L.L. Haan, and A. Ferreira, Extreme Value Theory., Springer, 2006.
[http://dx.doi.org/10.1007/0-387-34471-3] ]. Clearly seen from Fig. (8 ), the data from plot (a) to (i) meet this prerequisite, thus can be analyzed by EVT. Extreme loads can then be properly and effectively forecasted. However, plot (j) and (k) of Fig. (8
), the data from plot (a) to (i) meet this prerequisite, thus can be analyzed by EVT. Extreme loads can then be properly and effectively forecasted. However, plot (j) and (k) of Fig. (8 ) show that the torque of the engine and the generator are centralized in the large torque section under the engine-only mode, which do not conform to the prerequisite of EVT. This is determined by the working principle and internal control strategy of HEV: when the required torque constantly increases, the vehicle operates in the combined power mode with the motor being started; thus the engine can always work in the best efficiency. Considering that the overall value of the load within these two groups is small and centralized in the large load section, just a common statistical method can deal with these data. As shown in Fig. (8
) show that the torque of the engine and the generator are centralized in the large torque section under the engine-only mode, which do not conform to the prerequisite of EVT. This is determined by the working principle and internal control strategy of HEV: when the required torque constantly increases, the vehicle operates in the combined power mode with the motor being started; thus the engine can always work in the best efficiency. Considering that the overall value of the load within these two groups is small and centralized in the large load section, just a common statistical method can deal with these data. As shown in Fig. (8 ), the distributions of each terminal differ from one another when working under different operating modes. Thus the entire original data are definitely not independent, and these data are identically distributed random variables and cannot be directly fitted using GEV.
), the distributions of each terminal differ from one another when working under different operating modes. Thus the entire original data are definitely not independent, and these data are identically distributed random variables and cannot be directly fitted using GEV.
4.2. GEV Distribution and Extreme Loads
In order to analyze the data of Fig. (8a to i
to i ), suppose X1, X2, …, Xn are independent and are identically distributed random variables of one terminal under one specific mode. These variables subject to a distribution function F(x). For a natural number n, Mn represents the maximum load of random variables:
), suppose X1, X2, …, Xn are independent and are identically distributed random variables of one terminal under one specific mode. These variables subject to a distribution function F(x). For a natural number n, Mn represents the maximum load of random variables:
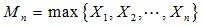 |
(1) |
Theoretically, Mn can be deduced by X1, X2, …, Xn as follows:
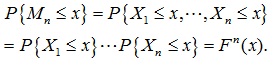 |
(2) |
However, the distribution function F(x) is usually unknown (Fig. 8 ). The direct application of this method is difficult. An effective method [6B. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire", Ann. Math., vol. 44, pp. 423-453, 1943.
). The direct application of this method is difficult. An effective method [6B. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire", Ann. Math., vol. 44, pp. 423-453, 1943.
[http://dx.doi.org/10.2307/1968974] ] is to first recognize that F(x) is unknown; the asymptotic model of Fn(x) is then used to study the extreme distribution of Mn. If the upper extreme point of distribution Fn (x) (x = sup{x: F(x) < 1}) is assumed to be x*, Fn (x) → ∞ for any x < x* when n → ∞. Mn converges to a degenerate distribution and can be standardized by the following equation:
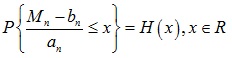 |
(3) |
 |
Fig. (8) Load distribution column diagrams of three terminals under different modes. |
where H(x) is a non-degenerate distribution. If the constant sequences an > 0 and bn exist, the distribution H(x) must belong to one of the following types [28M. R. Leadbetter, G. Lindgren, and H. Rootzen, Extremes and Related Properties of Random Sequences and Processes, Springer-Verlag: New York, December 1983.
[http://dx.doi.org/10.1007/978-1-4612-5449-2] ]:
Gumbel distribution:
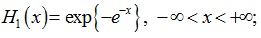 |
(4) |
Fréchet distribution:
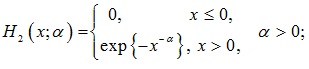 |
(5) |
Weibull Distribution:
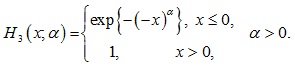 |
(6) |
The three types above of extreme value distribution functions can be merged into a unified expression, for short is GEV, to conveniently analyze the statistical problems [29A.F. Jenkinson, "The frequency distribution of the annual maximum (or minimum) values of meteorological elements", Q. J. R. Meteorol. Soc., vol. 81, pp. 158-171, 1955.
[http://dx.doi.org/10.1002/qj.49708134804] ].
Expression of the integrated distribution is:
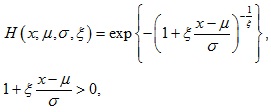 |
(7) |
where µ ϵ R is the location parameter, σ > 0 is the scale parameter, ξ ϵ R is the shape parameter or tail index. When ξ → 0, the distribution corresponds to a Gumbel distribution. x* is infinite and its tail exponentially decays. This distribution can be abbreviated as follows:
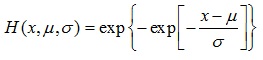 |
(8) |
When ξ > 0, the distribution corresponds to a Fréchet distribution. x* is also infinite and its tail decays in the form of a power function. When ξ < 0, the distribution corresponds to a Weibull distribution and x* is finite.
4.3. Fitting Results of Extreme Load Distribution
As seen in Fig. (9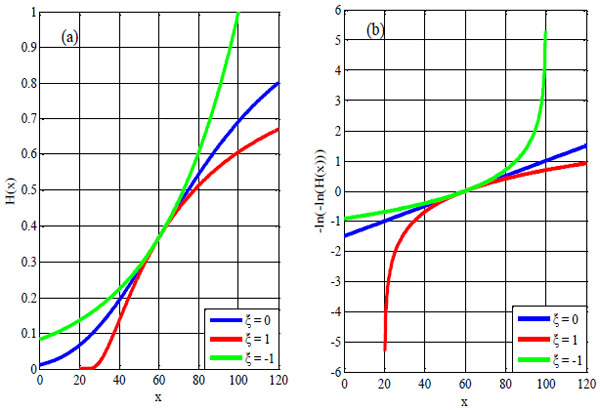 ), three types of extreme value distribution functions are plotted as H(X) vs. x and -ln(-ln(H(x))) vs. x. (Fig. 9
), three types of extreme value distribution functions are plotted as H(X) vs. x and -ln(-ln(H(x))) vs. x. (Fig. 9 ) (b) shows that the Gumbel distribution becomes a straight line, the Fréchet distribution (ξ > 0) is concave, and the Weibull distribution (ξ < 0) is convex. With these distribution types, the screened data of each mode belongs to can be clearly analyzed.
) (b) shows that the Gumbel distribution becomes a straight line, the Fréchet distribution (ξ > 0) is concave, and the Weibull distribution (ξ < 0) is convex. With these distribution types, the screened data of each mode belongs to can be clearly analyzed.
The fitting parameters and results estimated by the block maxima approach of the GEV are respectively shown in Table 2 and Fig. (10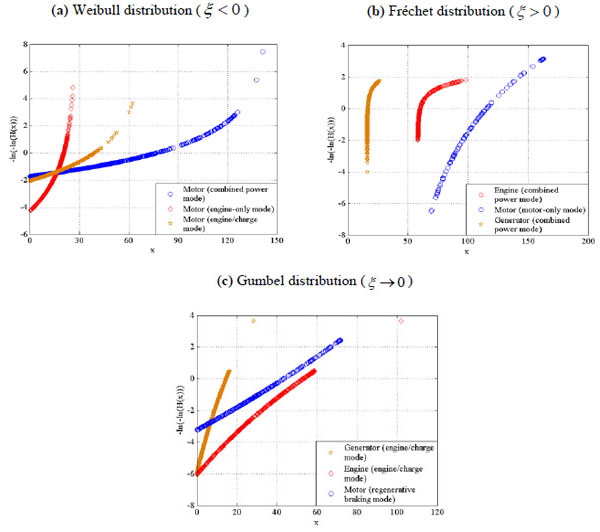 ). Each of these three distributions can be found in the extreme load distributions under different operating modes. (Fig. 10a
). Each of these three distributions can be found in the extreme load distributions under different operating modes. (Fig. 10a ) clearly shows that the loads of the motors under the combined power mode, the engine-only mode and the engine/charge modecorrespond to the Weibull distribution. (Fig. 10b
) clearly shows that the loads of the motors under the combined power mode, the engine-only mode and the engine/charge modecorrespond to the Weibull distribution. (Fig. 10b ) clearly shows that the loads of the motor under the motor-only mode, the engine under the combined power mode and the generator under the combined power mode correspond to the Fréchet distribution. In Fig. (10c
) clearly shows that the loads of the motor under the motor-only mode, the engine under the combined power mode and the generator under the combined power mode correspond to the Fréchet distribution. In Fig. (10c ), the loads of the motor under the regenerative braking mode, engine under the engine/charge mode and generator under the engine/charge mode correspond to the Gumbel distribution.
), the loads of the motor under the regenerative braking mode, engine under the engine/charge mode and generator under the engine/charge mode correspond to the Gumbel distribution.
For a certain distribution type, the specific distributions can also be different because of the parameter differences. As shown in Fig. (10a ), three distribution curves all correspond to Weibull distribution. However, shapes of three curves are different for that all three parameters (parameter ξ parameter μ and scale parameter σ) are different. The similar phnomenon is also exist in Fig. (10b
), three distribution curves all correspond to Weibull distribution. However, shapes of three curves are different for that all three parameters (parameter ξ parameter μ and scale parameter σ) are different. The similar phnomenon is also exist in Fig. (10b & c
& c ), which shows that not only the distribution type but also the parameters will decide the load distribution, but the former is the basis.
), which shows that not only the distribution type but also the parameters will decide the load distribution, but the former is the basis.
DISCUSSIONS
In the field of engineering, especially the HEV where the mode switches exist frequently, the distributions of the extreme values might be considered separately under different working modes. Traditionally, only one distribution is selected fit the load, which will lead to large deviations due to the unsuitable distribution. This paper focuses on the issue and combines three different distributions as a unified expression named GEV. In Fig. (9 ), shapes of the curves based on these three distributions have been presented and provide a visual path to distinguish them. With GEV, the fitting results present different shapes, and in Fig. (10
), shapes of the curves based on these three distributions have been presented and provide a visual path to distinguish them. With GEV, the fitting results present different shapes, and in Fig. (10 ), different shapes of the curves clearly illustrate that the extreme load in HEV under different modes should be fitted with different distributions and they should be selected based on the load characteristics. This research result contributes to prove the feasibility and necessity of MDAM in HEV and break the tradition of fitting the whole extreme value with one single distribution. The application of MDAM in HEV can improve the fitting accuracy of the extreme load with different distributions.
), different shapes of the curves clearly illustrate that the extreme load in HEV under different modes should be fitted with different distributions and they should be selected based on the load characteristics. This research result contributes to prove the feasibility and necessity of MDAM in HEV and break the tradition of fitting the whole extreme value with one single distribution. The application of MDAM in HEV can improve the fitting accuracy of the extreme load with different distributions.
 |
Fig. (9) Three different appearances of GEV diatributions (x: output torques). |
At the same time, the application of the method mentioned in this paper is not limited in the field of HEV, it can also be used in many other fields in engineering. For examples, similar to HEV, a loader has six operation sections, such as the spading section, the no load backward section, the load forward section and so on, the extreme loads on a half axle of the powertrain in a loader within different setions can be evaluated by MDAM. Operating objects of excavators also have many types, such as the primary soil, the disturbed soil, the finger stone and the big rocks, extreme loads due to different objects vary from each other, MDAM may be a considerable selection to evaluate the distributions of the extreme loads with different characteristics due to various objects.
 |
Fig. (10) Fitting results for all screened data (x: output torques). |
CONCLUSION
HEV usually operates in multimode conditions, and the load characteristics of each mode are different. Thus the original data are not independent and EVT cannot be directly applied. In order to prove the necessity of fitting the extreme value of HEV with different fitting distributions, the MDAM is proposed in this paper based on EVT to analyze the extreme loads of HEV. The simulated data are screened and classified into five typical operating modes according to the working principle and driving mechanism of HEV. The data of each mode are analyzed using GEV, and the conclusions obtained are as follows:
- In different modes, the original load distribution of each terminal varies.
- The loads of the motor (motor-only mode), engine (combined power mode) and generator (combined power mode) correspond to the Fréchet distribution. The loads of the motor (regenerative braking mode), engine (engine/charge mode) and the generator (engine/charge mode) correspond to the Gumbel distribution. The loads of the motors (combined power mode, engine-only mode and engine/charge mode) correspond to the Weibull distribution. These extreme value distributions all appear in the extreme load distribution of each terminal under different modes.
- Although the shape parameters of several modes are approximately equal, the location parameters and scale parameters differ because of different original distributions. This difference results in the difference of extreme value distributions.
Distribution fittings of extreme loads highly decide the load extrapolation results, as well as the latter analysis based on the extrapolated load spectrum. Research results in this paper provide a new thought to estimate the distributions of the extreme load in HEV and powerfully illustrates the necessity and possibility of MDAM.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was supported by National Natural Science Foundation of China (No. 51375202).
REFERENCES
| [1] | C.P. Przybyla, and D.L. Mcdowell, "Simulated microstructure-sensitive extreme value probabilities for high cycle fatigue of duplex Ti–6Al–4V", Int. J. Plast., vol. 27, pp. 1871-1895, 2011. [http://dx.doi.org/10.1016/j.ijplas.2011.01.006] |
| [2] | J.X. Wang, N.X. Wang, Z.Y. Wang, Y.S. Zhang, and L. Liu, "Determination of the minimum sample size for the transmission load of a wheel loader based on multi-criteria decision-making technology", J. Terramechs., vol. 49, pp. 147-160, 2012. [http://dx.doi.org/10.1016/j.jterra.2012.02.001] |
| [3] | J. Petit, and C. Sarrazin-Baudoux, "Some critical aspects of low rate fatigue crack propagation in metallic materials", Int. J. Fatigue, vol. 32, pp. 962-970, 2010. [http://dx.doi.org/10.1016/j.ijfatigue.2009.10.013] |
| [4] | T.A. Sawaguchi, G. Kausträter, A. Yawny, M. Wagner, and G. Eggeler, "Crack initiation and propagation in 50.9 at. pct Ni-Ti pseudoelastic shape-memory wires in bending-rotation fatigue", Metall. Mater. Trans., A Phys. Metall. Mater. Sci., vol. 34, pp. 2847-2860, 2003. [http://dx.doi.org/10.1007/s11661-003-0186-x] |
| [5] | A. Sawaguchi, G. Kausträter, A. Yawny, M. Wagner, and G. Eggeler, "Crack initiation and propagation in 50.9 at. pct Ni-Ti pseudoelastic shape-memory wires in bending-rotation fatigue", Tran. A, vol. vol. 34, 2003pp. 2847-2860 [http://dx.doi.org/10.1007/s11661-003-0186-x] |
| [6] | B. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire", Ann. Math., vol. 44, pp. 423-453, 1943. [http://dx.doi.org/10.2307/1968974] |
| [7] | A. Naess, O. Gaidai, and O. Batsevych, "Extreme value statistics of combined load effect processes", Struct. Saf., vol. 31, pp. 298-305, 2009. [http://dx.doi.org/10.1016/j.strusafe.2008.09.004] |
| [8] | R. Mínguez, Y. Guanche, and F.J. Méndez, "Point-in-time and extreme-value probability simulation technique for engineering design", Struct. Saf., vol. 41, pp. 29-36, 2013. [http://dx.doi.org/10.1016/j.strusafe.2012.10.002] |
| [9] | M. Behzad, and M. Mohsen, "A spatio-temporal dynamic regression model for extreme wind speeds", Extremes, vol. 17, pp. 221-245, 2014. [http://dx.doi.org/10.1007/s10687-014-0180-2] |
| [10] | N. Chini, and P.K. Stansby, "Extreme values of coastal wave overtopping accounting for climate change and sea level rise", Coast. Eng., vol. 65, pp. 27-37, 2012. [http://dx.doi.org/10.1016/j.coastaleng.2012.02.009] |
| [11] | E.J. Burke, J. Perry, and S.J. Brown, "An extreme value analysis of UK drought and projections of change in the future", J. Hydrol. (Amst.), vol. 388, pp. 131-143, 2010. [http://dx.doi.org/10.1016/j.jhydrol.2010.04.035] |
| [12] | P. Willems, A. Guillou, and J. Beirlant, "Bias correction in hydrologic GPD based extreme value analysis by means of a slowly varying function", J. Hydrol. (Amst.), vol. 338, pp. 221-236, 2007. [http://dx.doi.org/10.1016/j.jhydrol.2007.02.035] |
| [13] | H. Sawsan, P. Ser-Huang, and T. Jonathan, "Portfolio risk assessment using multivariate extreme value methods", Extremes, vol. 17, pp. 531-556, 2014. [http://dx.doi.org/10.1007/s10687-014-0194-9] |
| [14] | D. Chen, T.T. Mao, X.Q. Pan, and T.Z. Hu, "Extreme value behavior of aggregate dependent risks", Insur. Math. Econ., vol. 50, pp. 99-108, 2012. [http://dx.doi.org/10.1016/j.insmatheco.2011.10.008] |
| [15] | A. K. Singh, D.E. Allen, and P.J. Robert, "Extreme market risk and extreme value theory", Math. Comput. Simulat., vol. 94, pp. 310-328, 2013. |
| [16] | R. Mínguez, M. Menéndez, F.J. Méndez, and I.J. Losada, "Sensitivity analysis of time-dependent generalized extreme value models for ocean climate variables", Adv. Water Resour., vol. 33, pp. 833-845, 2010. [http://dx.doi.org/10.1016/j.advwatres.2010.05.003] |
| [17] | A. Hurairah, N.A. Ibrahim, I.B. Daud, and K. Haron, "An application of a new extreme value distribution to air pollution data", Manage. Environ. Qual, Inter. J., vol. 16, pp. 17-25, 2005. [http://dx.doi.org/10.1108/14777830510574317] |
| [18] | C. Marty, and J. Blanchet, "Long-term changes in annual maximum snow depth and snowfall in Switzerland based on extreme value statistics", Clim. Change, vol. 111, pp. 705-721, 2012. [http://dx.doi.org/10.1007/s10584-011-0159-9] |
| [19] | V. Lucarini, D. Faranda, G. Turchetti, and S. Vaienti, "Extreme value theory for singular measures, Chaos: An interdisciplinary", J. Nonlinear Sci., vol. 22, pp. 1-16, 2012. |
| [20] | C.C. Caprani, and E.J. Obrien, "The use of predictive likelihood to estimate the distribution of estimate the distribution of extreme bridge traffic load effect", Struct. Saf., vol. 32, pp. 138-144, 2010. [http://dx.doi.org/10.1016/j.strusafe.2009.09.001] |
| [21] | M. Kasperski, and R. Hoxey, "Extreme-value analysis for observed peak pressures on the Silsoe cube", J. Wind Eng. Ind. Aerodyn., vol. 96, pp. 994-1002, 2008. [http://dx.doi.org/10.1016/j.jweia.2007.06.024] |
| [22] | J. Ekengren, and J. Bergström, "Extreme value distributions of inclusions in six steels", Extremes, vol. 15, pp. 257-265, 2012. [http://dx.doi.org/10.1007/s10687-011-0139-5] |
| [23] | C. J. Orie, and Q. I. Nwatu, "Challenges of energy saving crisis as a panacea to hybrid electric vehicle (HEV)", Mediterranean J. Soc. Sci., vol. 2, November 2011. |
| [24] | Toyota Motor Corporation, TOYOTA Hybrid System THS II, May 2003. |
| [25] | A.K. Gupta, and C.P. Ramanarayanan, "Analysis of circulating power within hybrid electric vehicle transmissions", Mechanism Mach. Theory, vol. 64, pp. 131-143, 2013. [http://dx.doi.org/10.1016/j.mechmachtheory.2013.01.011] |
| [26] | Z. Zou, D. Scott, B. Kevin, O'. Michael, H. Terry, R. Robert, W. Steve, and V. K. Sharma, "A new composite drive cycle for heavy-duty hybrid electric class 4-6 vehicles", SAE Trans., vol. 113, pp. 771-778, 2004. |
| [27] | L.L. Haan, and A. Ferreira, Extreme Value Theory., Springer, 2006. [http://dx.doi.org/10.1007/0-387-34471-3] |
| [28] | M. R. Leadbetter, G. Lindgren, and H. Rootzen, Extremes and Related Properties of Random Sequences and Processes, Springer-Verlag: New York, December 1983. [http://dx.doi.org/10.1007/978-1-4612-5449-2] |
| [29] | A.F. Jenkinson, "The frequency distribution of the annual maximum (or minimum) values of meteorological elements", Q. J. R. Meteorol. Soc., vol. 81, pp. 158-171, 1955. [http://dx.doi.org/10.1002/qj.49708134804] |






