- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mechanical Engineering Journal
(Discontinued)
ISSN: 1874-155X ― Volume 14, 2020
New Generation Geometrical Product Specification (GPS) Backed Flatness Error Estimation and Uncertainty Analysis
Muhammad Ilyas Khan*, Shuyuan Ma
Abstract
Measurement and verification are one of the prime stages in the entire course of geometrical products in new generation of geometrical product specifications (GPS) standard. Like other kinds of form tolerances, flatness error is one of the important characteristics affecting the functionality and quality of machined components; sufficient efforts have long been made to determine the flatness error close to the true value based on the minimum zone method (MZM) and still needs continual improvement. This paper presents real coded genetic algorithms referred as Efficient Genetic Algorithms (EGA) for flatness error based on minimum zone method having good precision, repeatability and fast convergence rate. This paper also presents evaluation procedure for measurement uncertainty in flatness error based on new generation geometrical product specifications (GPS). Uncertainty in flatness error has been determined and evaluation procedure is provided to prove the conformance or non-conformance by taking into account the uncertainty in measurement. The contributing factors in measurement uncertainties have been identified and then quantified. The flatness error and evaluation theory in this paper are in the framework of new generation GPS standard. Two practical examples have been presented to show the effectiveness of EGA and shed some light on the uncertainty evaluation theory based on new generation GPS standard.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 66
Last Page: 78
Publisher Id: TOMEJ-10-66
DOI: 10.2174/1874155X01610010066
Article History:
Received Date: 4/7/2014Revision Received Date: 5/10/2015
Acceptance Date: 10/10/2015
Electronic publication date: 29/04/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the School of Mechanical Engineering, Beijing Institute of Technology (BIT), Beijing, China; Tel: +8618810324915; Fax: +86 10 68914256; E-mail: milyas75@gmail.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 4-7-2014 |
Original Manuscript | New Generation Geometrical Product Specification (GPS) Backed Flatness Error Estimation and Uncertainty Analysis | |
INTRODUCTION
New generation of geometrical product specifications (GPS) incorporates the whole geometrical products from researches across development, design, manufacturing, and measurement/verification to its delivery, exploitation and maintenance [1P. Heping, and J. Xiangqian, "Evaluation and management procedure of measurement uncertainty in new generation geometrical product specification (GPS)", Measurement, vol. 42, no. 5, pp. 653-660, 2009.
[http://dx.doi.org/10.1016/j.measurement.2008.10.009] ]. Like other geometrical characteristics, flatness has long been remained as an important icon in engineering design and manufacturing which directly affects the quality and functionality of the machined components. A number of researches have been conducted and still needs continual improvement to measure the flatness error as close as possible to the accurate value. The flatness measurement is performed to gauge the quality of machined components with reference to established standards and specifications. In order to produce technically and economically efficient components, manufacturers are making efforts to correct the imperfections in the production process, and to accurately and precisely measure the forms errors.
To cope with the increasing demand of manufacturing automation, fast measuring instruments have been developed. These instruments include. Coordinate measuring machines (CMM), interferometers, roundness testers etc. These equipments are supported by computer which controls the mechanical movements and calculates tolerance evaluation of the measured data. To measure the critical parameters of the components geometrical features, data taken with CMM or any other three dimensional measuring equipment must be processed by proper algorithms to evaluate the geometrical features such as flatness, based on minimum zone method [2Geometrical Product Specifications (Gps) - Flatness -part 1:Vocabulary and Parameters of Flatness, Iso 12781-1, International Organization for Standardization: Geneva, 2011.].
New generation of GPS [2Geometrical Product Specifications (Gps) - Flatness -part 1:Vocabulary and Parameters of Flatness, Iso 12781-1, International Organization for Standardization: Geneva, 2011.] defines two types of reference planes known as least square reference plane and minimum zone reference plane, corresponding to these reference planes, there are two approaches for flatness error estimation formally known as least square method (LSM) and minimum zone method (MZM). Least square method [3H.Y. Tseng, "A genetic algorithm for assessing flatness in automated manufacturing systems", J. Intell. Manuf., vol. 17, no. 3, pp. 301-306, 2006.
[http://dx.doi.org/10.1007/s10845-005-0004-y] ] is widely encouraged due to computational ease, but LSM results in overestimation of the result leading to the rejection of qualified components. Numerous algorithms have been developed for the flatness error. These algorithms are compromised of computational ease, computation time and accuracy.
Minimum zone method is exploited for the sake of accuracy. Flatness error determination based on minimum zone method is not a linear problem and cannot be approached by exploiting simple linear mathematical techniques. In order to solve highly non-linear problems for flatness error, different optimization techniques have been utilized, like Particle swarm Optimization (PSO) [4C. Cui, T. Li, L.A. Blunt, X. Jiang, H. Huang, R. Ye, and W. Fan, "The assessment of straightness and flatness errors using particle swarm optimization", Proc. CIRP, vol. 10, pp. 271-275, 2013.
[http://dx.doi.org/10.1016/j.procir.2013.08.041] ], genetic algorithm [5C. Cui, B. Li, F. Huang, and R. Zhang, "Genetic algorithm-based form error evaluation", Meas. Sci. Technol., vol. 18, no. 7, p. 1818, 2007.
[http://dx.doi.org/10.1088/0957-0233/18/7/004] -10T. Weber, S. Motavalli, B. Fallahi, and S.H. Cheraghi, "A unified approach to form error evaluation", Precis. Eng., vol. 26, no. 3, p. 269, 2002.
[http://dx.doi.org/10.1016/S0141-6359(02)00105-8] ], computational geometry based approaches [11J. Huang, "An efficient approach for solving the straightness and the flatness problems at large number of data points", Comput. Aided Des., vol. 35, no. 1, pp. 15-25, 2003.
[http://dx.doi.org/10.1016/S0010-4485(01)00172-5] -13G.L. Samuel, and M.S. Shunmugam, "Evaluation of straightness and flatness error using computational geometric techniques", Comput. Aided Des., vol. 31, no. 13, pp. 829-843, 1999.
[http://dx.doi.org/10.1016/S0010-4485(99)00071-8] ] etc.
In order to achieve more accurate and precise results, new generation GPS takes into account the uncertainties in measurement to prove the conformance and non-conformance of the measured part.
New generation GPS standard has introduced three types of uncertainties, namely measurement uncertainty, correlation uncertainty and specification uncertainty. The designer is accountable for quantification of correlation and specification uncertainty and the metrologist is accountable for the quantification of measurement uncertainty [1P. Heping, and J. Xiangqian, "Evaluation and management procedure of measurement uncertainty in new generation geometrical product specification (GPS)", Measurement, vol. 42, no. 5, pp. 653-660, 2009.
[http://dx.doi.org/10.1016/j.measurement.2008.10.009] ].
To implement new generation GPS standard effectively and to have reliable results in measurement, three standards ISO 14253-1 [14 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 1: Decision Rules for Proving Conformance or Non-conformance with Specifications, Iso 14253-1, International Organization for Standardization: Geneva, 2013.], ISO 14253-2 [15 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011.] and ISO 14253-3 [16Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 3: Guidelines for Achieving Agreements on Measurement Uncertainty Statements, Iso 14253-3, International Organization for Standardization: Geneva, 2011.] play leading roles in the quality and reliability of measurement results. ISO 14253-1 outlines the decision rules for proving conformance or non-conformance with specifications after taking into account the uncertainty in measurement results and is the legal contract between manufacturer and end user. ISO 14253-2 provides guidelines to quantification of uncertainty in measurement, calibration of measurement equipments and product verification. ISO 14253-3 provides the guidelines for achieving agreement on measurement uncertainty.
The difference between the true and measured value is the measurement error. The true value cannot be measured perfectly; however, an attempt can be made to approach the true value. In order to have reliable results and to solve this problem, uncertainty in measurement should overcome the measurement errors; however, traditional methods exploited in the past do not guarantee the reliability of the results and are not in conformity with the new generation GPS standard.
In order to fill this gap, genetic algorithms referred as efficient genetic algorithms for flatness error according to ISO 12781-1 [2Geometrical Product Specifications (Gps) - Flatness -part 1:Vocabulary and Parameters of Flatness, Iso 12781-1, International Organization for Standardization: Geneva, 2011.] using minimum zone method has been developed and measurement uncertainty has been determined on the basis of new generation geometrical product specification. Conformance and non-conformance have been determined according to ISO 14253-1 [14 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 1: Decision Rules for Proving Conformance or Non-conformance with Specifications, Iso 14253-1, International Organization for Standardization: Geneva, 2013.], sources of measurement uncertainties have been identified and quantified according to ISO14253-2 [15 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011.] and solution is sought by referring to ISO 14253-3 [16Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 3: Guidelines for Achieving Agreements on Measurement Uncertainty Statements, Iso 14253-3, International Organization for Standardization: Geneva, 2011.]. The entire process from flatness definition to analysis is in the framework of new generation GPS standard.
The paper provided the mathematical model of flatness error based on minimum zone method (MZM), the proposed genetic algorithms, measurement uncertainty determination, experimental work, discussions and results and finally conclusions are drawn.
MATHEMATICAL MODEL FOR FLATNESS ERROR
Flatness can be defined as the state of a surface having all features in one plane and flatness tolerance based on minimum zone method can be defined by two parallel planes in such a way that all the extracted points must lie inside the two parallel planes with a smallest possible distance [2Geometrical Product Specifications (Gps) - Flatness -part 1:Vocabulary and Parameters of Flatness, Iso 12781-1, International Organization for Standardization: Geneva, 2011.].
Consider a set of n0 data points, pi (xi,yi,zi) where extracted from a plane part, as per definition of flatness [2Geometrical Product Specifications (Gps) - Flatness -part 1:Vocabulary and Parameters of Flatness, Iso 12781-1, International Organization for Standardization: Geneva, 2011.]; assume one of the parallel planes is:
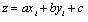 |
(1) |
The distance di from the data points pi (xi,yi,zi) to the parallel plane is:
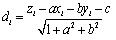 |
(2) |
Let f be the minimum separation between the two planes, then:
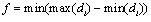 |
(3) |
The problem is highly non-linear as the minimum separation f depends upon parameters (a,b). In Eq. 3; f is the flatness error, also known as cost function in optimization terminology and is subjected to the constraints [17X.M. Yang, H. Liu, P. Guan, and L. Zhang, "Evaluation of the axial end flatness error based on genetic algorithm", Adv. Mat. Res., vol. 230, pp. 329-333, 2011.
[http://dx.doi.org/10.4028/www.scientific.net/AMR.230-232.329] ].
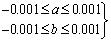 |
(4) |
PROPOSED GENETIC ALGORITHMS
The mathematical model presented in the above section is a highly non-linear optimization problem. In order to take over such non-linear complex optimization problems, genetic algorithms [18D.B. Fogel, "An introduction to simulated evolutionary optimization", IEEE Trans. Neural Netw., vol. 5, no. 1, pp. 3-14, 1994.
[http://dx.doi.org/10.1109/72.265956] [PMID: 18267775] , 19J.H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, U Michigan Press: USA, 1975.] play a vital role by providing solution to such problems.
The objective is to determine the minimum value of cost function i.e. minimum separation of the two planes to satisfy the minimum zone method [2Geometrical Product Specifications (Gps) - Flatness -part 1:Vocabulary and Parameters of Flatness, Iso 12781-1, International Organization for Standardization: Geneva, 2011.]. The algorithms parameters include, initial population size, maximum number of generations ( maxgen ) selection, crossover, elitism, and mutation.
To develop algorithms for flatness error evaluation, an array of population is triggered of some random values. Let v be the population size and w as the number of variables, then the normalized random values r of matrix pnorm is generated.
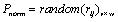 |
(5) |
The population size v is set to 40 in the proposed EGA. The number of variables, w=2 (‘a’ and ‘b’ from Eq. 2). The generated pnorm consists of random values between 0 and 1 and these values are required to be in the range of the constraints of the variables of Eq. 4 [20R.L. Haupt, and S.E. Haupt, Practical Genetic Algorithms, John Wiley & Sons: USA, 2004.], this process is known as un-normalization.
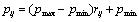 |
(6) |
where, pmax and pmin are the upper and lower bounds of the constraints (from Eq. 4), respectively. p=(pij)vxw is the unnormalized matrix of pnorm and is the initial population of (a,b) The flatness error f is determined by using experimental data and initial population P by using Eq. 3.
In the proposed algorithms, selection rate is kept at 50% i.e. half of the flatness values and their corresponding plane coefficients determined above are selected using Roulette wheel method [21E.G. Shopova, and N.G. Vaklieva-Bancheva, "BASIC-A genetic algorithm for engineering problems solution", Comput. Chem. Eng., vol. 30, no. 8, pp. 1293-1309, 2006.
[http://dx.doi.org/10.1016/j.compchemeng.2006.03.003] ] and rest of the half are discarded.
Roulette wheel method has one inherited problem that sometime it does not select the best value of f from the pool and therefore smooth convergence do not occurs in next generations. In order to solve this problem, Elitism [22D.A. Coley, An Introduction to Genetic Algorithms for Scientists and Engineers, World Scientific: Singapore, 1999.
[http://dx.doi.org/10.1142/3904] ] is implemented which copies the best values of f along with their corresponding coefficients from the previous generation and replaces them with the worst values in the current generation, leading to the smooth convergence.
Parents are generated from the 50% values using Roulette wheel method [21E.G. Shopova, and N.G. Vaklieva-Bancheva, "BASIC-A genetic algorithm for engineering problems solution", Comput. Chem. Eng., vol. 30, no. 8, pp. 1293-1309, 2006.
[http://dx.doi.org/10.1016/j.compchemeng.2006.03.003] ]. After parent’s generation (pairing), mating has been performed using blended crossover [21E.G. Shopova, and N.G. Vaklieva-Bancheva, "BASIC-A genetic algorithm for engineering problems solution", Comput. Chem. Eng., vol. 30, no. 8, pp. 1293-1309, 2006.
[http://dx.doi.org/10.1016/j.compchemeng.2006.03.003] ] with 50% crossover rate. If p1 and p2 are parent chromosomes, the offspring’s chromosomes are expressed as:
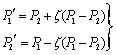 |
(7) |
where determined as follows:
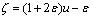 |
(8) |
In Eq. 8, random number u is generated for each gene with a uniform distribution in the interval. The parameter ε is set as basic GA local parameter; value 0.5 is selected as a value for GA local parameter. After crossover new offspring’s are added to the population.
After crossover, mutation is performed. Non-uniform mutation has the capability to fine local tuning and is exploited where a high accuracy is desired. Non-uniform mutation has been utilized in the proposed algorithm [23Z. Michalewicz, Genetic Algorithms+ Data Structures= Evolution Programs, Springer: USA, 1996.
[http://dx.doi.org/10.1007/978-3-662-03315-9] ]. The non-uniform mutation is governed by Eqs. 9 and 10 [23Z. Michalewicz, Genetic Algorithms+ Data Structures= Evolution Programs, Springer: USA, 1996.
[http://dx.doi.org/10.1007/978-3-662-03315-9] ]. For a given parent, if the element pm is selected for mutation randomly, the resulting mutated offspring is 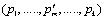 , where
, where 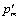 is selected from the two possible choices according to Eq. 9.
is selected from the two possible choices according to Eq. 9.
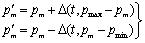 |
(9) |
In Eq. 9, first part of the equation is applicable if random digit generated is 0 and second part is applicable if random digit generated is 1, pmax and pmin are upper and lower bounds for pm (from Eq. 4); pm is selected for mutation randomly. The function Δ(t,y) returns a value in the range (0, y). Let t be the current generation, maxgen as the maximum number of generation, β the random value between [0,1], q as the degree of non-uniformity then:
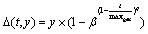 |
(10) |
The degree of non-uniformity q has been kept equal to 1 [21E.G. Shopova, and N.G. Vaklieva-Bancheva, "BASIC-A genetic algorithm for engineering problems solution", Comput. Chem. Eng., vol. 30, no. 8, pp. 1293-1309, 2006.
[http://dx.doi.org/10.1016/j.compchemeng.2006.03.003] ] and by increasing the value of q the average rate of decreasing of the step size becomes smaller [24X. Zhao, X.S. Gao, and Z.C. Hu, "Evolutionary programming based on non-uniform mutation", Appl. Math. Comput., vol. 192, no. 1, pp. 1-11, 2007.
[http://dx.doi.org/10.1016/j.amc.2006.06.107] ].
After non-uniform mutation, chromosomes are replaced with mutated chromosomes with 10% mutation rate; the flatness error (cost function, Eq. 3) is determined and then ranked in ascending order based on cost function f (Eq. 3). The first evaluation generation is completed and algorithms advances for the next generation to find the best solution. The program terminates as the maximum number of generation is achieved. Maximum number of generation (maxgen) is set to 50 in the proposed algorithms.
MEASUREMENT UNCERTAINTY DETERMINATION
To calculate the uncertainty in the flatness error based on new generation GPS standard, model function is required. The propagation and correlation coefficients must be determined. The law of propagation of uncertainty is [1P. Heping, and J. Xiangqian, "Evaluation and management procedure of measurement uncertainty in new generation geometrical product specification (GPS)", Measurement, vol. 42, no. 5, pp. 653-660, 2009.
[http://dx.doi.org/10.1016/j.measurement.2008.10.009] ].
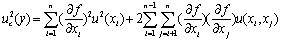 |
(11) |
In Eq. 11, 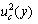 shows the variance of measurement result, the square root of
shows the variance of measurement result, the square root of 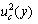 is the standard uncertainty; u(xi,xj) shows the covariance between ‘xi’ and ‘xj’; partial derivatives,
is the standard uncertainty; u(xi,xj) shows the covariance between ‘xi’ and ‘xj’; partial derivatives, 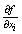 are called influence coefficients; u2(xi) shows the variance of the input data and square root of the variance of u2(xi) is the estimate of the standard deviation about the mean value and calculated as:
are called influence coefficients; u2(xi) shows the variance of the input data and square root of the variance of u2(xi) is the estimate of the standard deviation about the mean value and calculated as:
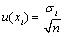 |
(12) |
In Eq. 12, σi is the standard deviation of the samples based on n measurements (i=1,2,3,...,n) of individual contributing component. According to ISO 14253-2 [15 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011.], if calculated standard deviation is based on few number of readings, the standard deviation may be incorrect and may be too small. For this purpose, a safety factor h, is multiplied with standard deviation. The safety factor h varies according to the sample size [15 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011.], so Eq. 12 can be modified as:
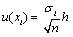 |
(13) |
Suppose the two peak values (maximum and minimum) are P1(x1,y1,z1) & P2(x2,y2,z2), then from Eq. 3, the minimum separation is:
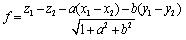 |
(14) |
Applying Eq. 11 on Eq. 14, the variance of measurement result is:
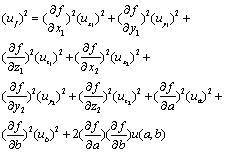 |
(15) |
In Eq. 15, uf is the standard uncertainty in the flatness error, u(a,b) is the covariance and is obviously considered that correlation exists between ‘a’ and ‘b’.
The influence coefficients are calculated by taking the derivatives of Eq. 14 as shown in Eq. 16, influence coefficients and covariance or second moment are calculated according to [25S.G. Rabinovich, Measurement Errors and Uncertainties, Springer: USA, 2005.].
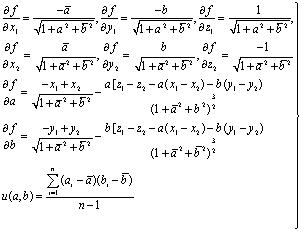 |
(16) |
In Eq. 16,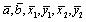 are the average values of a,b,x1,y1,x2 & y2, respectively.
are the average values of a,b,x1,y1,x2 & y2, respectively.
The expanded standard uncertainty (U) in flatness error is:
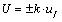 |
(17) |
According to ISO 14253-1 [14 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 1: Decision Rules for Proving Conformance or Non-conformance with Specifications, Iso 14253-1, International Organization for Standardization: Geneva, 2013.] the conformance, non-conformance and uncertainty zone (gray zone) can be achieved by adding expanded standard uncertainty to design flatness value i.e. fd±U where fd is the designed flatness value.
According to ISO 14253-2 [15 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011.], uncertainty in measurement usually results from measurement environment, instrument inherited errors etc. and required to be identified and then quantified. The normal uncertainty budgeting for the measurement taken based on new generation GPS standard is,
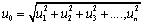 |
(18) |
In Eq. 18, are the individual sources of uncertainties arising from various sources such as environmental factors like temperature, inherited instrument limitations like repeatability, etc. and u0 is the overall uncertainty in each measured point. Eq. 18 holds good for uncorrelated components of uncertainties as there is no correlation between the individual sources. The expanded measurement uncertainty (U0) of measured point can be calculated as:
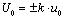 |
(19) |
In Eqs. 17 and 19, k is the coverage factor and k = 2 correspond to 95% confidence interval [1P. Heping, and J. Xiangqian, "Evaluation and management procedure of measurement uncertainty in new generation geometrical product specification (GPS)", Measurement, vol. 42, no. 5, pp. 653-660, 2009.
[http://dx.doi.org/10.1016/j.measurement.2008.10.009] ].
EXPERIMENTAL WORK
Roundness tester was exploited in the experimental work. The roundness tester was first adjusted according to the technical requirements.
The plane part was placed on the table top of the roundness tester and contour of plane part was measured in ‘x’ and ‘y’ directions (axis) to get values in ‘z’ direction (axis). ‘x’ direction data are taken by moving the horizontal arm (R-axis direction of roundness tester) while for the ‘y’ direction, the plane part moved manually. The resolution of roundness tester was adjusted to 0.0001mm. The contour of the plane part surface was measured by extracting sufficient number of data points closely representing the whole real surface of the plane part.
Two plane parts were inspected for flatness error and evaluation, each part of surface was checked five times at different positions. The first part of data set is referred to as data set-1 (from data sample 1 to 5) and the second part of data set is referred to as data set-2 (from data sample 6 to 10). The data set-1 and data set-2 are shown in Appendix.
RESULTS AND DISCUSSIONS
To verify the authenticity of the EGA algorithms, flatness error results were compared to other methods [6G. Deng, G. Wang, and J. Duan, "A new algorithm for evaluating form error: the valid characteristic point method with the rapidly contracted constraint zone", J. Mater. Process. Technol., vol. 139, no. 1, pp. 247-252, 2003.
[http://dx.doi.org/10.1016/S0924-0136(03)00229-2] , 8Y.M. Jiang, and G.X. Liu, "A new flatness evaluation-rotation method based on GA", Adv. Mat. Res., vol. 139, pp. 2033-2037, 2010.
[http://dx.doi.org/10.4028/www.scientific.net/AMR.139-141.2033] ]. Based on EGA, flatness error results were 0.00713mm and 0.02894mm for data points of [6G. Deng, G. Wang, and J. Duan, "A new algorithm for evaluating form error: the valid characteristic point method with the rapidly contracted constraint zone", J. Mater. Process. Technol., vol. 139, no. 1, pp. 247-252, 2003.
[http://dx.doi.org/10.1016/S0924-0136(03)00229-2] , 8Y.M. Jiang, and G.X. Liu, "A new flatness evaluation-rotation method based on GA", Adv. Mat. Res., vol. 139, pp. 2033-2037, 2010.
[http://dx.doi.org/10.4028/www.scientific.net/AMR.139-141.2033] ] respectively, and results of EGA are in complete agreement with [6G. Deng, G. Wang, and J. Duan, "A new algorithm for evaluating form error: the valid characteristic point method with the rapidly contracted constraint zone", J. Mater. Process. Technol., vol. 139, no. 1, pp. 247-252, 2003.
[http://dx.doi.org/10.1016/S0924-0136(03)00229-2] , 8Y.M. Jiang, and G.X. Liu, "A new flatness evaluation-rotation method based on GA", Adv. Mat. Res., vol. 139, pp. 2033-2037, 2010.
[http://dx.doi.org/10.4028/www.scientific.net/AMR.139-141.2033] ], this shows the authenticity of the EGA algorithms.
Along with accuracy, EGA has marked level of repeatability. Data from [6G. Deng, G. Wang, and J. Duan, "A new algorithm for evaluating form error: the valid characteristic point method with the rapidly contracted constraint zone", J. Mater. Process. Technol., vol. 139, no. 1, pp. 247-252, 2003.
[http://dx.doi.org/10.1016/S0924-0136(03)00229-2] ] was loaded in the proposed EGA five times to check the repeatability of the codes (EGA algorithm); the flatness error results were 0.007141mm, 0.007144mm, 0.007144mm, 0.007150mm, and 0.007137mm. When considering the last two digits, the flatness error results are found to be not valid according to the accuracy of the data set (as the resolution adjusted in the roundness tester to 0.0001mm) but the results indicate the marked degree of precision and repeatability of EGA.
A first plane part for flatness inspection with 0.01mm value of flatness (fd) is design, data set-1 belongs to the first plane part. Second plane part for flatness inspection with 0.02mm value of flatness (fd) is design, data set-2 belongs to the second plane part. Both plane part data were loaded in EGA, flatness error and their corresponding plane coefficients were determined as shown in Tables 1 and 2 for data set-1 and data set-2, respectively.
The optimization graph for data set-1 and data set-2 is shown in Figs. (1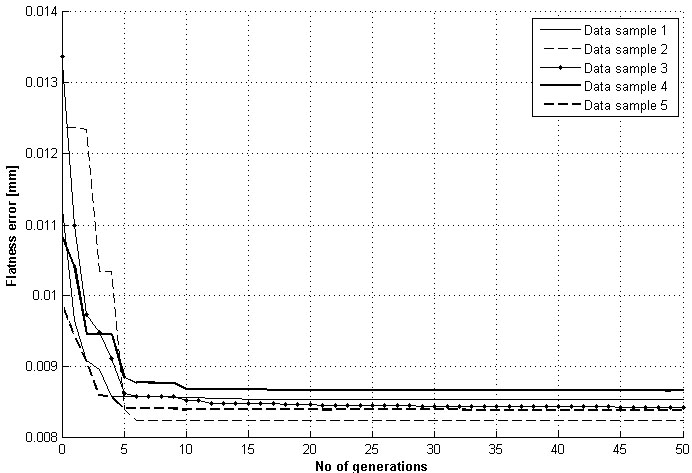 , 2
, 2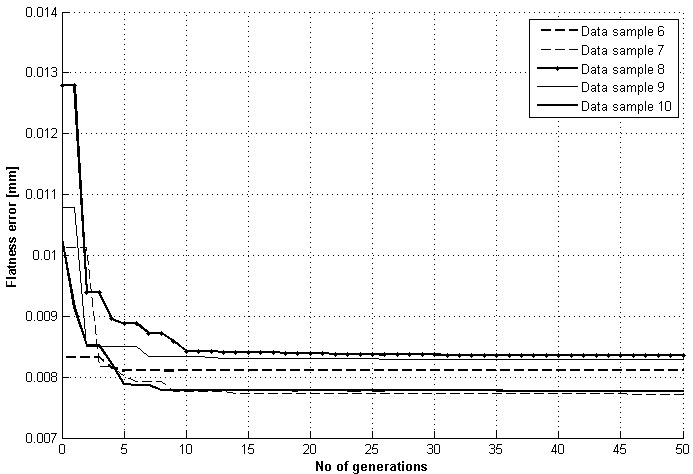 ) respectively, showing smooth convergence in less than twenty generations.
) respectively, showing smooth convergence in less than twenty generations.
By applying the series of uncertainty equations from Eq. 11 through Eq. 17, the expanded standard uncertainty in flatness error evaluation for data set-1 are, U=±0.0027mm and for data set-2 are U=±0.0048mm having coverage factor k =2 corresponding to confidence interval of 95% [1P. Heping, and J. Xiangqian, "Evaluation and management procedure of measurement uncertainty in new generation geometrical product specification (GPS)", Measurement, vol. 42, no. 5, pp. 653-660, 2009.
[http://dx.doi.org/10.1016/j.measurement.2008.10.009] ].
 |
Fig. (1) Optimization process of five data samples of data set-1. |
 |
Fig. (2) Optimization process of five data samples of data set-2. |
By applying ISO14253-1 [14 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 1: Decision Rules for Proving Conformance or Non-conformance with Specifications, Iso 14253-1, International Organization for Standardization: Geneva, 2013.], i.e. adding value of U to design value; three zones are created, namely conformance zone, non-conformance zone and uncertainty zone (gray zone). After adding the uncertainty values in the fd, the average flatness error values fall in uncertainty zone for data set-1 and in conformance zone for data set-2 as shown in Fig. (3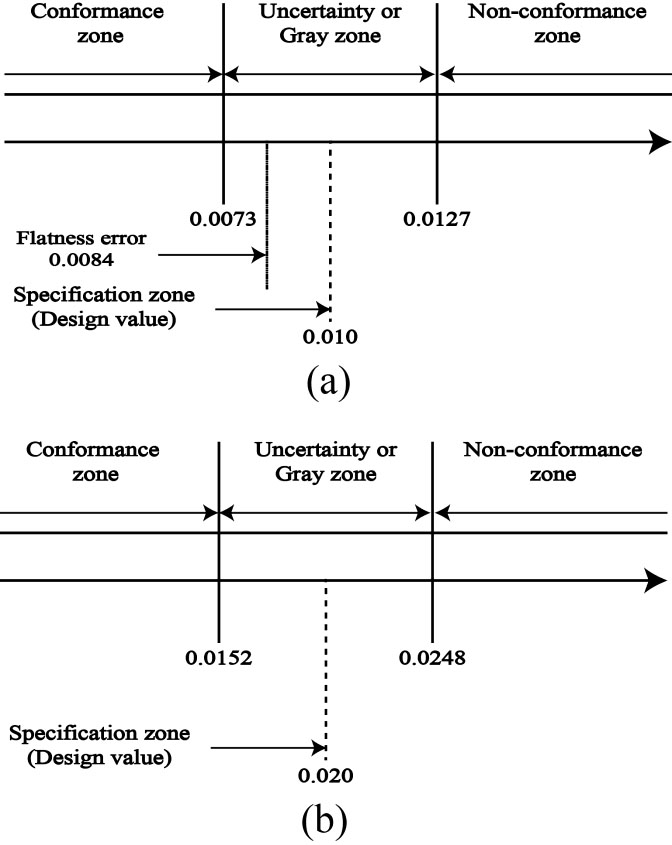 ), respectively.
), respectively.
According to ISO14253-2 [15 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011.], measurement uncertainty results from different external sources like measurement environment, humidity etc. and internal sources like repeatability of measuring instrument, drift etc. As roundness tester was used in the measurement for extracting the contour of the plane part surface, the potential contributor of measurement uncertainty includes:
 |
Fig. (3) Flatness error result [mm] assessment of data set-1 (a) and data set-2 (b). |
Repeatability and Resolution (ur)
The repeatability study has been conducted and uncertainty components (ur1) calculated as (assuming normal distribution) 0.02μm. The roundness tester adjusted to 0.1μm resolution (dr). Considering rectangular distribution, the uncertainty due to resolution (ur2) is:
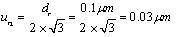
According to ISO14253-2 [15 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011.], the greatest contribution factor will be selected between both contributing factors, so measurement uncertainty for ur is ur2=ur=0.03µm
Axis Error (ux)
Axis error covers the straightness error of the two axes in X and Y planes, according to the manufacturer the error (de) in both axes of roundness tester is 1μm in full range, considering rectangular distribution, the uncertainties due to axis error are:
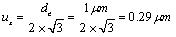
Temperature (ut)
Temperature is the major environmental source of error in any measurement [26A. Gusel, B. Acko, and V. Mudronja, "Measurement uncertainty in calibration of measurement surface plates flatness", J. Mech. Eng., vol. 55, no. 5, pp. 1-7, 2009. UDC 621.7.08:531.7]. According to new generation GPS, the temperature requirement for measurement is 20±2C˚. The experimental work was performed in a highly controlled condition and by taking the thermal coefficient of materials and variation in temperature, the length change due to temperature is 0.38μm. Considering uniform distribution:
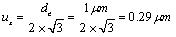
Drift in Roundness Tester (ud)
The drift study conducted against the time which requires completing one set of measurement for flatness error and the drift in the system, ud found is 0.03μm.
As the all components above are uncorrelated, the uncertainty in each measurement point is calculated according to Eq. 18 which is 0.4µm, the expanded uncertainty budget according to Eq. 19 is 0.8μm.
According to the above results and analysis, results of flatness error are in complete agreement with other methods [6G. Deng, G. Wang, and J. Duan, "A new algorithm for evaluating form error: the valid characteristic point method with the rapidly contracted constraint zone", J. Mater. Process. Technol., vol. 139, no. 1, pp. 247-252, 2003.
[http://dx.doi.org/10.1016/S0924-0136(03)00229-2] , 8Y.M. Jiang, and G.X. Liu, "A new flatness evaluation-rotation method based on GA", Adv. Mat. Res., vol. 139, pp. 2033-2037, 2010.
[http://dx.doi.org/10.4028/www.scientific.net/AMR.139-141.2033] ], the difference of five calculations are 0.5μm for first data set and 0.7μm for second data set as shown in Tables 1 and 2, respectively. This difference is mainly caused by random error in each data set and different measurement positions. The convergence rate is higher than other methods; the solution converges in less than twenty generations as shown in Figs. (1, 2). The codes have been marked repeatability.
By adding the uncertainty with the design values (fd); three zones are created, conformance zone, uncertainty zone (gray zone) and non-conformance zone. Table 1 shows that average flatness error is 0.0084mm; this value is larger than conformance and fall in gray zone as shown in Fig. (3a ). If the values fall in gray zone, the customer cannot accept the work piece and supplier cannot reject the work piece leading to a conflict between the supplier and customer. In order to cope with such potential conflict, ISO 14253-3 [16Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 3: Guidelines for Achieving Agreements on Measurement Uncertainty Statements, Iso 14253-3, International Organization for Standardization: Geneva, 2011.] provides guidelines over uncertainty values. Table 2 shows that average flatness error is 0.0081mm; this value falls in conformance zone and according to ISO 14253-1 [14 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 1: Decision Rules for Proving Conformance or Non-conformance with Specifications, Iso 14253-1, International Organization for Standardization: Geneva, 2013.], the components are acceptable if the values fall in conformance zone and rejected if the values fall in non-conformance zone.
). If the values fall in gray zone, the customer cannot accept the work piece and supplier cannot reject the work piece leading to a conflict between the supplier and customer. In order to cope with such potential conflict, ISO 14253-3 [16Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 3: Guidelines for Achieving Agreements on Measurement Uncertainty Statements, Iso 14253-3, International Organization for Standardization: Geneva, 2011.] provides guidelines over uncertainty values. Table 2 shows that average flatness error is 0.0081mm; this value falls in conformance zone and according to ISO 14253-1 [14 Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 1: Decision Rules for Proving Conformance or Non-conformance with Specifications, Iso 14253-1, International Organization for Standardization: Geneva, 2013.], the components are acceptable if the values fall in conformance zone and rejected if the values fall in non-conformance zone.
The above two scenarios show that uncertainty has a sufficient influence on measurement results. In data set-1 the flatness error is 0.0084mm. Although the part is acceptable without considering uncertainty but uncertainty has squeezed the conformance zone and the result has been dragged into the uncertainty zone, thereby making the measurement results controversial.
CONCLUSION
Measurement and uncertainty are one of the prime steps in new generation GPS system.The paper proposed a new method for evaluating flatness error with customized algorithms named as Efficient Genetic Algorithms (EGA). The experimental results of the proposed EGA algorithms indicate several advantages in precision, repeatability and fast convergence over other algorithms. High precision and repeatability lead to the reduction of uncertainties due to algorithms. Elitism is implemented to EGA algorithms which avoid the loss of best solution by roulette wheel selection method ensuring current best state of flatness error. The constraints are incorporated in initial population leading to fast mature convergence in less than twenty generations. The EGA algorithms are independent of number of data points and converge in same time and number of generations. The proposed algorithms not only give the result of flatness error according to new generation of GPS standard but also directions of the plane.
Uncertainties in measurement are one of the prime part in new generation GPS standard. New generation of GPS standard takes into account the measurement uncertainty to prove conformance and non-conformance of the flatness error. By circumventing measurement uncertainty in any measurement process may lead to the acceptance of rejected or controversial components. The first part (data set-1) analysis indicates that even if the measurement result is below the design value but by considering uncertainty the conformance zone can be shrunk due to uncertainty and the part cannot be accepted. This indicates that uncertainty has sufficient influence on measurement result.
This is also concluded that measurement and uncertainty evaluation performed using new generation GPS ensure the authenticity and reliability of the result.
The EGA may be extended to the estimation of other form and location tolerances with slight modifications.
APPENDIX: EXPERIMENTAL MEASUREMENT DATA
[Units: x-axis, y-axis [mm], z-axis [μm], data set-1 [data sample 1~5]; data set-2[data sample 6~10]]
| Data Sample 1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | |||||||||||
| 5 | 8 | 13 | 18 | 23 | 28 | 33 | 38 | 43 | 48 | 53 | 55 | |
| 5.5 | -1.6 | -2.1 | -1.5 | -1.7 | -2.6 | -1.3 | -1.4 | -2.2 | -1.8 | -1.5 | -2.1 | -2.2 |
| 10.5 | -8.6 | -10.9 | -9.1 | -9.6 | -9.9 | -10.1 | -9.4 | -9.9 | -10.8 | -9.5 | -10.3 | -10.6 |
| 15.5 | -13.6 | -14.7 | -13.8 | -12.6 | -12.8 | -13.5 | -13.3 | -13.3 | -14.1 | -12.8 | -13.6 | -13.8 |
| 20.5 | -15.1 | -14.3 | -15 | -13.2 | -13.5 | -13.5 | -13.9 | -13 | -12.8 | -12.3 | -13.3 | -13.2 |
| 25.5 | -10.8 | -12.1 | -12.2 | -11.2 | -10.9 | -11 | -11.4 | -11.7 | -11.8 | -11.7 | -11.8 | -11.6 |
| 30.5 | -20.2 | -20.7 | -20.4 | -19.8 | -20.8 | -19.9 | -20.3 | -19.7 | -19.8 | -19.8 | -20.9 | -20.6 |
| 35 | -19.4 | -20.2 | -19.6 | -19.2 | -19.5 | -19 | -19.7 | -19.6 | -19.8 | -18.9 | -19.2 | -19.3 |
| Data Sample 2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | |||||||||||
| 5 | 10 | 13 | 18 | 23 | 28 | 33 | 38 | 43 | 48 | 53 | 55 | |
| 5 | -0.3 | -2.4 | -2.2 | -1.4 | -1.4 | -3.1 | -2.2 | -0.7 | -1.9 | -2.3 | -1.3 | -2.5 |
| 10 | -8 | -8.7 | -9.7 | -9.2 | -7.9 | -8.6 | -8 | -7.7 | -9 | -7.7 | -8.4 | -7.9 |
| 15 | -11.2 | -12.8 | -12.1 | -12.6 | -11.5 | -11 | -11.9 | -12.9 | -12.6 | -11.8 | -12.1 | -12.2 |
| 20 | -11.3 | -13.3 | -12.1 | -11.8 | -12.3 | -11.8 | -12.4 | -11.6 | -12.7 | -12.2 | -11.7 | -12.3 |
| 25 | -8.7 | -10.5 | -9.9 | -9.8 | -10.1 | -10.8 | -10.7 | -9.9 | -10.4 | -10.1 | -9.8 | -10 |
| 30 | -14.2 | -14.9 | -15.8 | -15.3 | -15.5 | -16.9 | -17.4 | -17.9 | -17.4 | -17.5 | -17.2 | -17.6 |
| 35 | -16.2 | -17.5 | -18.1 | -17.7 | -18.5 | -19.5 | -19.3 | -18.6 | -17.9 | -17.7 | -17.6 | -17.6 |
| Data Sample 3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | ||||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | |
| 5 | -1.5 | -4 | -3 | -2.6 | -0.9 | -0.6 | 0.3 | 0.1 | 0.2 | 0.3 | -0.6 |
| 10 | -8.7 | -9.7 | -8.9 | -8.7 | -8.6 | -8 | -7.2 | -6.1 | -6.3 | -7.3 | -6.9 |
| 15 | -13.2 | -13.4 | -12.5 | -12 | -11.9 | -10.4 | -10.8 | -9.9 | -10.5 | -11.1 | -11.8 |
| 20 | -13.9 | -15.1 | -14.5 | -13.7 | -12 | -10.7 | -11 | -10.9 | -11.1 | -11 | -10.9 |
| 25 | -11.2 | -12.5 | -11.7 | -10.9 | -9.7 | -8.9 | -8.7 | -8.3 | -8.7 | -8.9 | -9.2 |
| 30 | -15.9 | -16.9 | -15.9 | -14.8 | -15.3 | -14.8 | -13.3 | -12.7 | -13.1 | -13.4 | -17.4 |
| 35 | -18.9 | -19.1 | -19.1 | -18.1 | -16.9 | -16.6 | -16.1 | -15.3 | -15.6 | -16.3 | -17.4 |
| Data Sample 4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | ||||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | |
| 5.5 | -3.4 | -4.4 | -3.7 | -3.2 | -4.5 | -3.5 | -2.7 | -3.6 | -4.3 | -2.6 | -2.8 |
| 10.5 | -10.1 | -10.1 | -10.7 | -10 | -9.7 | -9.8 | -8.9 | -10.1 | -9.8 | -9.7 | -9.1 |
| 15.5 | -15 | -15.5 | -15 | -14.3 | -15.9 | -15.1 | -15.3 | -13.4 | -13.7 | -14.4 | -15.3 |
| 20.5 | -14.3 | -15.9 | -14.1 | -14.9 | -13.7 | -13.7 | -15.1 | -13.9 | -13.7 | -14.7 | -14.8 |
| 25.5 | -12 | -12.2 | -13 | -11.7 | -12.4 | -12.4 | -12 | -11.6 | -12.6 | -12.7 | -12.5 |
| 30.5 | -21.7 | -22 | -21.2 | -21.1 | -20.7 | -20.5 | -20.8 | -19.2 | -20.6 | -20.9 | -22 |
| 35 | -20.5 | -21.5 | -20 | -20.5 | -19.6 | -20.3 | -20.9 | -19.1 | -19.2 | -20.7 | -20.2 |
| Data Sample 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | ||||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | |
| 5 | -2.2 | -3.1 | -3.7 | -3.9 | -1.9 | -2 | -2.6 | -3.1 | -3.4 | -2.1 | -2.3 |
| 8 | -6.5 | -7.6 | -7.2 | -6.2 | -7.2 | -6.4 | -5.8 | -6.3 | -6.8 | -6.9 | -6.8 |
| 12 | -10.8 | -11.6 | -11.4 | -11 | -11.5 | -10.7 | -10.8 | -11.7 | -11.2 | -11 | -11 |
| 16 | -14.9 | -14.9 | -14.2 | -14.1 | -15.6 | -14.5 | -14.5 | -13.2 | -14.7 | -14.3 | -14.2 |
| 20 | -13.1 | -13.7 | -13.7 | -14.9 | -14.2 | -14.1 | -13.4 | -13.5 | -13.8 | -14.4 | -15 |
| 23 | -13.9 | -13.9 | -13.1 | -14.2 | -12.7 | -14.2 | -13.2 | -13.8 | -13.5 | -13.7 | -13.6 |
| 28 | -16.1 | -14.8 | -13 | -13.1 | -13 | -14.3 | -14.6 | -14.4 | -14.2 | -13.6 | -14.3 |
| 32 | -20.3 | -19.7 | -18.6 | -19.9 | -18.9 | -17.9 | -20.1 | -18.2 | -18 | -18.7 | -17.9 |
| 35 | -20 | -19.4 | -18.7 | -18.6 | -18.9 | -19.2 | -19.1 | -18.9 | -18.9 | -18.5 | -19 |
| Data Sample 6 | ||||||||
|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | |||||||
| 4 | 6 | 10 | 14 | 18 | 22 | 26 | 28 | |
| 5 | 2.7 | 2.8 | 4.4 | 5.8 | 5.5 | 7.4 | 6.9 | 7.7 |
| 10.5 | -2.6 | -2.2 | -2 | -0.5 | 0.2 | 0.3 | 0.4 | 1.9 |
| 15.5 | -3.6 | -3.4 | -3.4 | -3 | -2.3 | -1 | 0 | 0.3 |
| 20.5 | -1.7 | -1.8 | -0.7 | -0.4 | 0.3 | 0.7 | 1.1 | 2.5 |
| 25.5 | 1.8 | 1.6 | 2.5 | 3.6 | 4 | 4.3 | 4.8 | 5.9 |
| 30.5 | -6.2 | -6.6 | -5.2 | -4.6 | -3.8 | -3.9 | -2.3 | -2.2 |
| 35 | -3.1 | -3 | -2.8 | -2.3 | -0.9 | 0 | 0.5 | 0.5 |
| Data Sample 7 | ||||||||
|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | |||||||
| 4 | 6 | 10 | 14 | 18 | 22 | 26 | 28 | |
| 5 | 6.8 | 5.7 | 6.2 | 8.1 | 8.4 | 9 | 7.1 | 8.8 |
| 10 | 0.7 | 0.7 | 1.8 | 2.2 | 3.1 | 3.5 | 3.8 | 4 |
| 15 | 0.2 | 0.4 | 1 | 0.7 | 0.3 | 2.5 | 2.9 | 2.8 |
| 20 | 1.5 | 1.9 | 2.1 | 2.7 | 3.4 | 4.4 | 3.8 | 4.7 |
| 25 | 5.6 | 5.9 | 5.6 | 6.6 | 7.4 | 7.8 | 7.7 | 8.7 |
| 30 | -0.3 | -0.2 | 0.2 | 0.7 | 1.5 | 1.7 | 2.2 | 2.6 |
| 35 | 0.4 | 0.3 | 0.7 | 0.9 | 1.4 | 2.1 | 2.8 | 2.3 |
| Data Sample 8 | |||||||
|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | ||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | |
| 5 | 4.5 | 4.2 | 4 | 3.8 | 6.8 | 6.4 | 7.3 |
| 10.5 | 0 | -0.4 | 0.3 | 0.6 | 3 | 3 | 3.4 |
| 15.5 | -3.5 | -2.4 | -1.3 | -2.7 | 0.2 | 0 | 0.4 |
| 20.5 | -0.4 | 0.1 | 0.3 | 1.3 | 1.7 | 2.5 | 3.4 |
| 25.5 | 2.5 | 3.2 | 4.5 | 4.5 | 5.7 | 4.9 | 6.2 |
| 30.5 | -4.9 | -4.5 | -3.9 | -3.3 | -1.8 | -2.1 | -1.3 |
| 35 | -2.1 | -1.9 | -1.2 | -0.4 | 0.1 | 0.9 | 1.3 |
| Data Sample 9 | |||||||
|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | ||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | |
| 5 | 6.8 | 7.2 | 8.9 | 7.7 | 10.4 | 9.9 | 10.9 |
| 10.4 | 2.5 | 3.6 | 3.7 | 4.8 | 5 | 6.2 | 6.1 |
| 15.3 | 0.6 | 1.3 | 2.9 | 3.1 | 4.6 | 4.2 | 5.4 |
| 20.2 | 3.1 | 4.3 | 4.4 | 4 | 5.3 | 6.2 | 6.4 |
| 25.1 | 7.1 | 7.5 | 8.7 | 8.1 | 9.6 | 10.1 | 10.9 |
| 30.4 | -1.5 | 3.6 | -0.2 | 0.3 | 3.8 | 1.6 | 4.4 |
| 35 | 2 | 2.3 | 3.2 | 3.3 | 4.3 | 4.7 | 5.4 |
| Data Sample 10 | ||||||||
|---|---|---|---|---|---|---|---|---|
| x-Axis | y-Axis | |||||||
| 4 | 8 | 10 | 12 | 18 | 20 | 24 | 28 | |
| 5 | 2.6 | 3.5 | 5.8 | 3.3 | 5.3 | 6.7 | 5.7 | 7.8 |
| 8 | 1.5 | 1.6 | 3.9 | 4.1 | 3.9 | 0.5 | 4.8 | 5.5 |
| 12 | -1.5 | -1.3 | -0.6 | -2.2 | -1.3 | 0.2 | 3.5 | 3.9 |
| 16 | -2 | -2.7 | 4 | 3.5 | 3.1 | 5.1 | -0.5 | 1.7 |
| 20 | -1.2 | -2.4 | -0.9 | 2.8 | 3.5 | 4 | 3.2 | 7.3 |
| 30 | -2.3 | -0.7 | -2.5 | -2.8 | -3 | 1 | 1.6 | 2 |
| 35 | -1.9 | -1.7 | -1.2 | -0.7 | -0.2 | 0.6 | 1.3 | 1.9 |
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This research work was supported by National Natural Science Foundation of China (Grant No. 51375052).
REFERENCES
| [1] | P. Heping, and J. Xiangqian, "Evaluation and management procedure of measurement uncertainty in new generation geometrical product specification (GPS)", Measurement, vol. 42, no. 5, pp. 653-660, 2009. [http://dx.doi.org/10.1016/j.measurement.2008.10.009] |
| [2] | Geometrical Product Specifications (Gps) - Flatness -part 1:Vocabulary and Parameters of Flatness, Iso 12781-1, International Organization for Standardization: Geneva, 2011. |
| [3] | H.Y. Tseng, "A genetic algorithm for assessing flatness in automated manufacturing systems", J. Intell. Manuf., vol. 17, no. 3, pp. 301-306, 2006. [http://dx.doi.org/10.1007/s10845-005-0004-y] |
| [4] | C. Cui, T. Li, L.A. Blunt, X. Jiang, H. Huang, R. Ye, and W. Fan, "The assessment of straightness and flatness errors using particle swarm optimization", Proc. CIRP, vol. 10, pp. 271-275, 2013. [http://dx.doi.org/10.1016/j.procir.2013.08.041] |
| [5] | C. Cui, B. Li, F. Huang, and R. Zhang, "Genetic algorithm-based form error evaluation", Meas. Sci. Technol., vol. 18, no. 7, p. 1818, 2007. [http://dx.doi.org/10.1088/0957-0233/18/7/004] |
| [6] | G. Deng, G. Wang, and J. Duan, "A new algorithm for evaluating form error: the valid characteristic point method with the rapidly contracted constraint zone", J. Mater. Process. Technol., vol. 139, no. 1, pp. 247-252, 2003. [http://dx.doi.org/10.1016/S0924-0136(03)00229-2] |
| [7] | R. Sharma, K. Rajagopal, and S. Anand, "A genetic algorithm based approach for robust evaluation of form tolerances", J. Manuf. Syst., vol. 19, no. 1, pp. 46-57, 2000. [http://dx.doi.org/10.1016/S0278-6125(00)88889-5] |
| [8] | Y.M. Jiang, and G.X. Liu, "A new flatness evaluation-rotation method based on GA", Adv. Mat. Res., vol. 139, pp. 2033-2037, 2010. [http://dx.doi.org/10.4028/www.scientific.net/AMR.139-141.2033] |
| [9] | X. Zhu, and H. Ding, "Flatness tolerance evaluation: an approximate minimum zone solution", Comput. Aided Des., vol. 34, no. 9, pp. 655-664, 2002. [http://dx.doi.org/10.1016/S0010-4485(01)00137-3] |
| [10] | T. Weber, S. Motavalli, B. Fallahi, and S.H. Cheraghi, "A unified approach to form error evaluation", Precis. Eng., vol. 26, no. 3, p. 269, 2002. [http://dx.doi.org/10.1016/S0141-6359(02)00105-8] |
| [11] | J. Huang, "An efficient approach for solving the straightness and the flatness problems at large number of data points", Comput. Aided Des., vol. 35, no. 1, pp. 15-25, 2003. [http://dx.doi.org/10.1016/S0010-4485(01)00172-5] |
| [12] | M.K. Lee, "An enhanced convex-hull edge method for flatness tolerance evaluation", Comput. Aided Des., vol. 41, no. 12, p. 930, 2009. [http://dx.doi.org/10.1016/j.cad.2009.06.011] |
| [13] | G.L. Samuel, and M.S. Shunmugam, "Evaluation of straightness and flatness error using computational geometric techniques", Comput. Aided Des., vol. 31, no. 13, pp. 829-843, 1999. [http://dx.doi.org/10.1016/S0010-4485(99)00071-8] |
| [14] | Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 1: Decision Rules for Proving Conformance or Non-conformance with Specifications, Iso 14253-1, International Organization for Standardization: Geneva, 2013. |
| [15] | Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 2: Guide to the Estimation of Uncertainty in Gps Measurement, in Calibration of Measuring Equipment and in Product Verification, Iso 14253-2, International Organization for Standardization: Geneva, 2011. |
| [16] | Geometrical Product Specification (Gps) - Inspection by Measurement of Workpieces and Measuring Equipment - Part 3: Guidelines for Achieving Agreements on Measurement Uncertainty Statements, Iso 14253-3, International Organization for Standardization: Geneva, 2011. |
| [17] | X.M. Yang, H. Liu, P. Guan, and L. Zhang, "Evaluation of the axial end flatness error based on genetic algorithm", Adv. Mat. Res., vol. 230, pp. 329-333, 2011. [http://dx.doi.org/10.4028/www.scientific.net/AMR.230-232.329] |
| [18] | D.B. Fogel, "An introduction to simulated evolutionary optimization", IEEE Trans. Neural Netw., vol. 5, no. 1, pp. 3-14, 1994. [http://dx.doi.org/10.1109/72.265956] [PMID: 18267775] |
| [19] | J.H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, U Michigan Press: USA, 1975. |
| [20] | R.L. Haupt, and S.E. Haupt, Practical Genetic Algorithms, John Wiley & Sons: USA, 2004. |
| [21] | E.G. Shopova, and N.G. Vaklieva-Bancheva, "BASIC-A genetic algorithm for engineering problems solution", Comput. Chem. Eng., vol. 30, no. 8, pp. 1293-1309, 2006. [http://dx.doi.org/10.1016/j.compchemeng.2006.03.003] |
| [22] | D.A. Coley, An Introduction to Genetic Algorithms for Scientists and Engineers, World Scientific: Singapore, 1999. [http://dx.doi.org/10.1142/3904] |
| [23] | Z. Michalewicz, Genetic Algorithms+ Data Structures= Evolution Programs, Springer: USA, 1996. [http://dx.doi.org/10.1007/978-3-662-03315-9] |
| [24] | X. Zhao, X.S. Gao, and Z.C. Hu, "Evolutionary programming based on non-uniform mutation", Appl. Math. Comput., vol. 192, no. 1, pp. 1-11, 2007. [http://dx.doi.org/10.1016/j.amc.2006.06.107] |
| [25] | S.G. Rabinovich, Measurement Errors and Uncertainties, Springer: USA, 2005. |
| [26] | A. Gusel, B. Acko, and V. Mudronja, "Measurement uncertainty in calibration of measurement surface plates flatness", J. Mech. Eng., vol. 55, no. 5, pp. 1-7, 2009. UDC 621.7.08:531.7 |





