- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Medical Informatics Journal
(Discontinued)
ISSN: 1874-4311 ― Volume 13, 2019
Mathematical Model of the Cupula-Endolymph System with Morphological Parameters for the Axolotl (Ambystoma tigrinum) Semicircular Canals
Rosario Vega1, Vladimir V Alexandrov2, 3, Tamara B Alexandrova1, 3, Enrique Soto*, 1
Abstract
By combining mathematical methods with the morphological analysis of the semicircular canals of the axolotl (Ambystoma tigrinum), a system of differential equations describing the mechanical coupling in the semicircular canals was obtained. The coefficients of this system have an explicit physiological meaning that allows for the introduction of morphological and dynamical parameters directly into the differential equations. The cupula of the semicircular canals was modeled both as a piston and as a membrane (diaphragm like), and the duct canals as toroids with two main regions: i) the semicircular canal duct and, ii) a larger diameter region corresponding to the ampulla and the utricle. The endolymph motion was described by the Navier-Stokes equations. The analysis of the model demonstrated that cupular behavior dynamics under periodic stimulation is equivalent in both the piston and the membrane cupular models, thus a general model in which the detailed cupular structure is not relevant was derived.
Article Information
Identifiers and Pagination:
Year: 2008Volume: 2
First Page: 138
Last Page: 148
Publisher Id: TOMINFOJ-2-138
DOI: 10.2174/1874431100802010138
Article History:
Received Date: 27/3/2008Revision Received Date: 23/5/2008
Acceptance Date: 23/6/2008
Electronic publication date: 26/8/2008
Collection year: 2008
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the Instituto de Fisiología – BUAP, Apartado Postal 406, Puebla, Pue. 72000, México; E-mail: esoto@siu.buap.mx
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 27-3-2008 |
Original Manuscript | Mathematical Model of the Cupula-Endolymph System with Morphological Parameters for the Axolotl (Ambystoma tigrinum) Semicircular Canals | |
1. INTRODUCTION
The processing of sensory information in the semicircular canals (SCs) of the vestibular system is accomplished through a diversity of structural and functional processes. These processes can be grouped in at least six compartments: a mechanical coupling mechanism, a mechanoelectrical transducer, a hair cell receptor potential generator, a neurotransmitter release compartment, a postsynaptic response mechanism, and a spike encoder (Fig. 1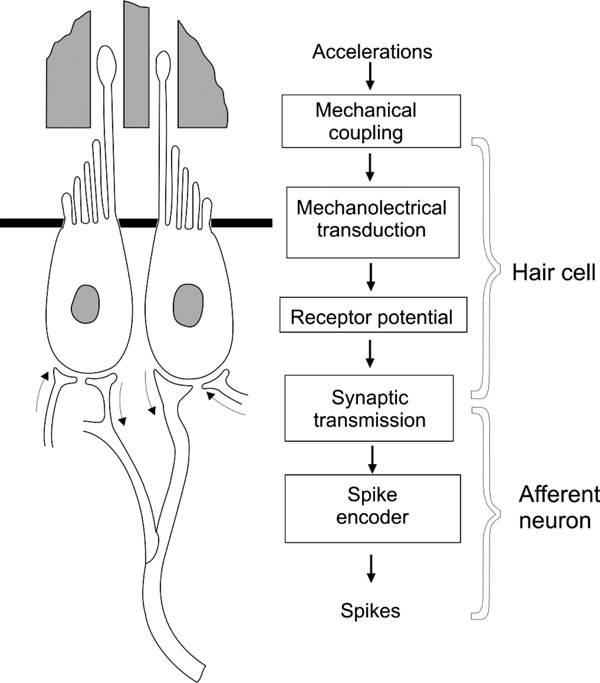 ). Modelling of this system, if considered in its minute details, would have an extreme complexity, making it practically impossible to operate. That is why we have decided to develop a series of synthetic compartmental models that will let us integrate the basic processes leading to the sensory coding of vestibular information.
). Modelling of this system, if considered in its minute details, would have an extreme complexity, making it practically impossible to operate. That is why we have decided to develop a series of synthetic compartmental models that will let us integrate the basic processes leading to the sensory coding of vestibular information.
Different technologies have recently been developed to function as part of vertical stabilization aids in humans [1Wangsong G, Merfeld DM. A prototype neural semicircular canal prosthesis using patterned electrical stimulation Ann Biomed Eng 2000; 28(5): 572-81.-3Tyler M, Danilov Y, Bach y, Rita P. Closing an open-loop control system: vestibular substitution through the tongue Proc J Integr Neurosci 2003; 2(2): 159-64.]. These devices could be particularly useful to contribute information to control the stand position in extreme situations (for example in human falling) and would also contribute to manage the space adaptation syndrome (SAS) [4Sadovnichii VA, Alexandrov VV, Lemak SS, Shkel AM. Vestibular function under extreme conditions of inertial navigation and its correction Moscow Univ Mech Bull 2003; 6: 46-54., 5]. Mathematical modelling of the vestibular endorgans is essential to develop adequate transfer functions and coding unit algorithms of these prosthetic devices.
In this work we concentrate our attention in the mechanical coupling of angular accelerations to the movement of the sensory cell hair bundles. The mechanical coupling largely determines the type of mechanical stimuli that is responsible for hair cell activation. Mechanical coupling properties determine that the utricle and the saccule could function as linear acceleration detectors, and the SCs as angular acceleration detectors, notwithstanding that both sensory organs are based on a very similar sensory cell type.
Mathematical modelling of the SCs mechanics is essentially based on Steinhausen's seminal work [6Steinhausen W. Uber die Beobachtung der cupula in den Bogengangsampullen des Labyrinthes des liebenden Hechts Pflugers Arch 1933; 232: 500-12.], who used a lineal model of the torsion pendulum to study the dynamics of the cupula-endolymph system [7Van Buskirk WC. The effect of the utricle on fluid flow in the semicircular canals Ann Biomed Eng 1977; 5: 1-11.-9Oman CM, Marcus EN, Curthoys IS. The influence of semicircular canal morphology on endolymph flow dynamics Acta Otolaryngol 1987; 103: 1-13.]. However, the model parameters are not strictly related to morphological measurements of the SCs; therefore, Steinhausen's model provides a general description of the SCs function but with poor predictability for specific systems.
Further developments of SC models were conducted in two main directions: i) improvement of the torsion pendulum model of Steinhausen and ii) elaboration of hydrodynamic models of the cupula-endolymph system.
The hydrodynamics of the SCs was first analyzed by Van Buskirk [10Van Buskirk WG, Watts RG, Liu YK. The fluid mechanics of the semicircular canals J Fluid Mech 1976; 78: 87-98.], who modeled the cupula as an elastic weightless membrane that spans the whole ampulla in the form of a diaphragm. Lately more detailed mathematical models of the cupula-endolymph system dynamics simulating the cupula as a diaphragm were also developed [11Rabbit RD, Damiano ER. A hydroelastic model of macromechanics in the endolymphatic vestibular canal J Fluid Mech 1992; 238: 337-69., 12Rabbitt RD. Directional coding of the dimensional movements by the vestibular semicircular canals Biol Cybern 1999; 80: 417-31.]. Other models have considered the cupula as a weighting elastic piston in an ideal liquid [13Curthoys IS, Oman CM. Dimensions of the horizontal semicircular duct, ampulla and utricle in human Acta Otolaryngol 1987; 103: 254-61., 14Kondrachuk AV, Sirenko SP, Shipov AA. Mathematical simulation of the gravity receptor Physiologist SupplV 1981; 34: S212-13.]. These last models have also considered the influence of varying SC forms on the dynamics of the cupula-endolymph system.
A combination of pendulum models and hydrodynamic analysis of the cupula-endolymph system has been accomplished by considering the system as composed by an elastic piston (cupula) in a viscous fluid (endolymph) [15Astakhova TG. Mathematical model of the semicircular canal of the vestibular system as an angular acceleration sensor Moscow Univ Mech Bull 1989; ser.1(No 1): 69-72. (in Russian), 16Astakhova TG. Mathematical model of the semicircular canal of the vestibular system PhD Thesis Moscow State University Lomonosov . 1990. (in Russian)]. As a result, the coefficients that are a non-lineal function of the morphological parameters of the SC system were obtained.
Most of the recent literature describe the details of the cupula-endolymph coupling process [9Oman CM, Marcus EN, Curthoys IS. The influence of semicircular canal morphology on endolymph flow dynamics Acta Otolaryngol 1987; 103: 1-13., 12Rabbitt RD. Directional coding of the dimensional movements by the vestibular semicircular canals Biol Cybern 1999; 80: 417-31., 17Damiano ER. A poroelastic continuum model of the cupula partition and the response dynamics of the vestibular semicircular canal J Biomech Eng 1999; 131: 449-60.], information transfer [9Oman CM, Marcus EN, Curthoys IS. The influence of semicircular canal morphology on endolymph flow dynamics Acta Otolaryngol 1987; 103: 1-13.] and coupling between the three semicircular canals [18Muller M, Verhagen JH. Optimization of the mechanical performance of a two-duct semicircular duct system- part 2 excitation of endolymph movements J Theor Biol 2002; 216(4): 425-.]. In this work we summarize a system of differential equations which has been previously presented in an extensive form [16Astakhova TG. Mathematical model of the semicircular canal of the vestibular system PhD Thesis Moscow State University Lomonosov . 1990. (in Russian), 19Alexandrov VV, Alexandrova TB, Astakhova TG, Yakushev AG, Soto E. Equations of the dynamics of the cupula-endolymph system in the semicircular canals Differ Equ 1999; 35(4): 1-6. (in Russian), 20Alexandrov VV, Astakhova TG, Trincher T. Mathematical modelling of the dynamics of the cupula-endolymph system Moscow Univ Mech Bull 1999; 54: 1-6.], and combine them with morphological data from the axolotl (Ambystoma tigrinum) inner ear to obtain a simplified model of the cupula-endolymph coupling mechanism. Results indicate that the theoretical analysis of the cupular mechanics modeled either as a diaphragm or as a piston produced analogous results when the system was subjected to a periodic stimulus. Based on this, a simplified mathematical model of the cupula-endolymph system was proposed. The advantage of using this model is that there is an explicit dependence of the model coefficients upon physiological and morphological parameters.
2. PHYSICAL AND MATHEMATICAL METHODS
An isolated semicircular canal of the vestibular apparatus can be considered as a thin curved tube filled with a viscous uncompressible fluid: the endolymph. Both ends of the tube are open and inserted into a sac (the utricle). One of the ends of the tube expands in the immediate neighborhood of the utricle, forming first an ampulla and then narrowing down to the initial diameter. The cupula (an elastic partition) lies inside the ampulla and is attached to the ampullary walls on the crista (a sensory base) in such a way that it is capable of shifting in response to motion of the endolymph within the canal. A subcupular space (a fluid interlayer ranging in thickness from 2 to 5 µm) forms between the cupula and the crista [21Kachar B, Parakkal M, Fex J. Structural basis for mechanical transduction in the frog vestibular sensory apparatus: I. The otolithic membrane Hear Res 1990; 45: 179-90.].
2.1. Dynamics of the Endolymph within the Rotating Semicircular Canal
Let us consider the endolymph dynamics in a semicircular canal of the toroidal form. Suppose a thin torus of outer radius a rotates about its axis with a given angular velocity ω(t). The Cartesian system XYZ with the origin O at the center of the torus is associated with the torus, which is formed by rotating the circle of radius a (lying in the plane XZ) about the Z-axis.
Let r and λ be the polar coordinates in the plane of the forming cross section of the torus and θ be the angular coordinate of this section being measured from the X-axis. Then, the coordinates r, λ, θ and x, y, z are related as follows:
The fluid motion in the torus is described by the Navier-Stokes equation
and by the continuity equation
Here V is the absolute velocity of the fluid, F is the mass-force vector, p is the fluid pressure, ρ is the density of the endolymph, μ is its viscosity, and v = μ/ρ is the fluid cinematic viscosity. Let us introduce the following dimensionless variables:
where R is external radius of semicircular canal and r is the internal radius of the semicircular canal duct.
Taking into account (3) and the formula F=0, we rewrite equation (1) in the form
The continuity equation (2) may be written down in the dimensionless form as follows:
Suppose u is the fluid velocity relative to the walls of the semircircular, ur, uλ are the transverse components of the relative velocity in the plane of the forming cross section of the torus, and u is the velocity component along the curved axis of the canal. Then,
Since the cross section of the canal is sufficiently small
its walls are smooth, and the appearance of secondary flows is improbable, we set
and simplify system (4) and (5) with regard to (3) and (6) If we ignore the terms of order ε 2, then from equation (6) we obtain
As a result, equations (4) take the form [2Shkel AM, Liu J, Ikei C, Zeng FG. Feasibility study on a prototype of vestibular implant using MEMS gyroscopes Proc Int IEEE Conf Sensors 2002; 55: 1526-31.]
See [5] for more detailed mathematical manipulations.
It is assumed that the symmetry of the flow with respect to the angle λ exists in system (8)-(10). Ignoring the terms of order ε2, from equations (8) and (10) we get
Turning back to the dimensional variables, we obtain
where
Thus, our analysis of motion of the endolymph within the toroidal rotating semicircular canal leads to solving equation (11) with the corresponding initial and boundary conditions. The pressure gradient
2.2. Mathematical Model of the Cupula-Membrane
Let us consider the semicircular canals as a toroid filled with a viscous incompressible fluid and rotating about its axis with angular velocity ω(t). If it is assumed that the cupula is a weighable membrane attached to the ampullary walls in such a way that the likelihood of fluid leakage is eliminated and that the cupula is an elastic diaphragm with density ρ, thickness 2δ, and stiffness T, by considering the transverse oscillations of the membrane when its displacement ξ (r, t) from the equilibrium position is directed perpendicularly to the plane of the undeflected membrane, the function ξ (r, t) defines a form of the membrane which is symmetric with respect to λ and has its maximal deflection when r = 0.
The transverse oscillations of the membrane are described by the equation
with the boundary conditions (in sections 2.2 and 2.3 a=a1=a0)
and with the corresponding initial conditions. Here Vt = ω R is the transient velocity of the canal, (p1–p2) is the pressure drop through the cupula, and the dot denotes the time differentiation. At the cupula
where L is the length of the semicircular canal duct. Dividing equation (13) by L ς and ignoring the terms of order
we obtain
2.3. Mathematical Model of the Cupula-Piston
If the cupula structure is conceived as a mobile piston with density ρ, width 2δ and height 2b, the balance between inertial forces, pressure difference on both sides of the piston, elastic forces of the piston and the frictional forces upon the lateral walls of the piston, will determine the movement of the piston in the canal (Fig. 2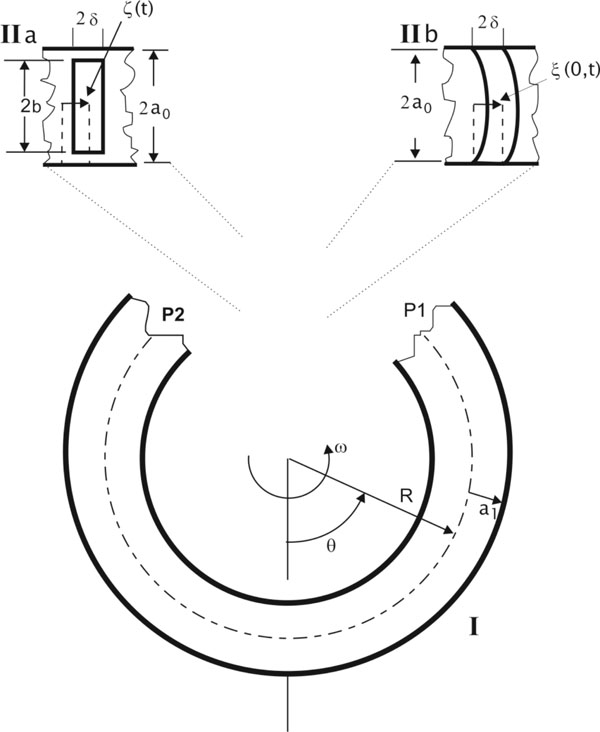 ):
):
where m0 is the mass of the piston, x its displacement with respect to the equilibrium point, γ is the elastic force coefficient that appears during the motion of the piston, (P1-P2) is the pressure difference between the sides of the cupula and F is the frictional viscous force at the lateral wall of the piston.
The dynamics of the cupula-endolymph system can be described by equations systems (11) and (15) when the cupula is like a piston and with the following boundary conditions:
The liquid flow can be divided into three different regions (Fig. 2 ). In region I (distant from the piston) the velocity distribution is assumed to be parabolic (this is correct for periodic stimuli (sin σt) with frequencies < 10Hz [22Damiano ER, Rabbit RD. A singular perturbation model of fluid dynamics in the vestibular semicircular canal and ampula J Fluid Mech 1996; 307: 333-72., 23]):
). In region I (distant from the piston) the velocity distribution is assumed to be parabolic (this is correct for periodic stimuli (sin σt) with frequencies < 10Hz [22Damiano ER, Rabbit RD. A singular perturbation model of fluid dynamics in the vestibular semicircular canal and ampula J Fluid Mech 1996; 307: 333-72., 23]):
where V1 is the mean velocity in region I. The velocity profile in the long-and-slender region of the duct is essentially Poseuille`s over the entire physiological frequency range [1Wangsong G, Merfeld DM. A prototype neural semicircular canal prosthesis using patterned electrical stimulation Ann Biomed Eng 2000; 28(5): 572-81.,8Oman CM, Young IR. The physiological range of pressure difference and cupula deflections in the human semicircular canal Acta Otolaryngol 1972; 74: 324-1.] if
Based on these assumptions the mathematical model of the SC with cupula-piston was developed.
The second region is near the piston (Fig. 2 ). Between regions II and I there is a transition zone. We consider that the pressure drop in this region can be negligible [11Rabbit RD, Damiano ER. A hydroelastic model of macromechanics in the endolymphatic vestibular canal J Fluid Mech 1992; 238: 337-69.]. Thence, pressure difference in the cap of the piston is the same as the pressure drop in region I which can be obtained from (11) and (17):
). Between regions II and I there is a transition zone. We consider that the pressure drop in this region can be negligible [11Rabbit RD, Damiano ER. A hydroelastic model of macromechanics in the endolymphatic vestibular canal J Fluid Mech 1992; 238: 337-69.]. Thence, pressure difference in the cap of the piston is the same as the pressure drop in region I which can be obtained from (11) and (17):
In the cleft between the piston and the crista ampullaris walls there is an abrupt change of pressure due to defective dynamical lubrication. Reynolds number calculated along the cleft was considered small. Thus, the calculation of the movement of endolymph through the cleft is based on the following equation:
where y = r – b, a≤r ≤ b, VII, is the mean velocity of endolymph flow in the cleft,
The solution of equation (19) is assumed to have the following form:
from initial and border conditions we obtain
hence the frictional force in the lateral surface of the piston is equal to:
where μ = vρ, and mean velocity in the lubricating layer
The coupled fluxes in regions II and I due to the pressure drop and constancy principle of flow in any section of the SC leads to two equations for the determination of two unknown functions V1(t) and C1(t), from where
Substituting (P1 – P2) from (8) into (5), F from (12) and assuming m = 2πb2δρ:
After transforming the system (25) and (26) to a non-dimensional form with the introduction of small parameters
where m is the endolymphatic mass.
A numerical analysis of models (14) to (27) will allow for the description of experimental results with measurements of the SC morphology to define parameters and account for specific cases.
3. MORPHOLOGICAL METHODS
Larval axolotls (Ambystoma tigrinum) weighting around 60 g were anesthetized with 3 aminobenzoic acid ethyl ester methasulfonate (MS-222) 0.1% for 10 min. The animals were decapitated and the lower jaw cut. The roof of the mouth was dissected and the otic capsule opened. Drops of fixing solution were placed in the otic capsule and the whole head of the animal was immersed in a cool (4°C) fixing solution for further isolation of the inner ear. The fixing solution was made of glutaraldehyde 2% or osmium 2% in 0.1 phosphate buffer and pH adjusted to 7.4 [25Glauter MA. Fixation, dehydration and embedding of biological specimens practical methods in electron microscopy. NY: Elsevier Sci 1987.]. Osmolarity of this solution was always 240 mOsm. When needed, sucrose was added in order to reach the optimal osmolarity value. Animal housing and experimental procedures were performed in accordance with the Helsinki guidelines.
The whole inner ear and its organs were inspected after fixation by stereomicroscopic observation and using rapid photographic proceedings [26Guzman-Flores CM, Alcaraz M, Fernández-Guardiola A. Procedimiento rápido para localizar electrodos en la neurofisiología experimental Bol Estud Med Biol 1958; 16: 26-31.]. In addition, osmium fixed preparations were placed in petri dishes containing phosphate buffer 0.1 mM and photographed under the stereomicroscope. For decalcification, the tissue was treated in a solution containing 1% nitric acid and 0.1% formaldehyde for 24 hr.
3.1. Optical Microscopy
For the optical microscopy analysis the inner ear was dissected separating the utricle, saccule, lagena, and SCs. Preparations were dehydrated and included in Spurr or Durcupan ACM synthetic resins.
Tissue segments were cut in a manual Porter-Blum ultramicrotome (Dupont, MT-1) using glass knives. Sections were of 1-2 µm. Slices were mounted on gelatinized slides and stained using toluidine blue 1% for 5-10 min. The tissue sections were rinsed, dried overnight and dehydrated in an ethanol series. Finally, they were dried, mounted with synthetic resin and analyzed in a light microscope (Zeiss Axioplan) and photographed with Kodak Ektachrome 100 and Tmax 100 film.
3.2. Scanning Electron Microscopy
Tissue was fixed either by Karnowsky fixative or with 2% osmium solution. Then, the inner ear was treated by the OTOTO technique as follows: the tissue segments were first immersed in a saturated solution of thiocarbohydrazide (20 min.) and then in a 1% osmium aqueous solution (2 hr). This procedure was repeated twice, thoroughly washing the preparations. After rinsing in the phosphate buffer solution, the preparations were carefully dissected in 70% alcohol. A jet of alcohol gently ejected from a pipette removed the otolith. Preparations were dehydrated in a graded ethanol series and dried by the critical point method using carbon dioxide.
Shortly before examination, some of the preparations were covered with nanometric silver film and observed in a Jeol (JSV-5400-LV) scanning electron microscope with a 10-30 KV voltage [27Soto E, Guevara J, Andrade J, Cruz-Vera R. Ultraestructura e inervación del oído interno en el axolotl (Ambystoma mexicanum), Segundo Congreso Mexicano de Microscopía Electrónica Cancún 1994; SSB14].
3.3. Morphometric Analysis
Micrographs were analyzed by using a digitizing tablet (Calcomp) and ad hoc software. The digital images were arranged and printed using Adobe Photoshop 4.0TM. Canal diameters were always measured by considering the smaller of their diameters. Dimensions of the SC crista were measured directly from the scanning electron and optical microscope micrographs. No correction for curvature or fixation induced shrinkage was performed. In order to calculate the volume of the endolymph into the SC ampulla it was assumed that ampullae have the form of an American football ball with their tips cut off. The volume of this structure is determined by obtaining data about its three axes: ampulla length, width and height (2a0). The ampulla width is equivalent to the crista large in Table 1. Then, by subtracting the volume of the crista ampullaris, the ampulla volume was calculated.
4. RESULTS
4.1. Morphological Results
While the anterior and lateral canals are elliptical with a maximum radius of 0.93 and 1.35 mm respectively, the posterior canal is quasi-circular with a radius of 0.89 mm. The duct radius was nearly the same in the three canals ≈ 150 µm.
The SC ampullae were identified as an enlargement of the SC duct (Fig. 3A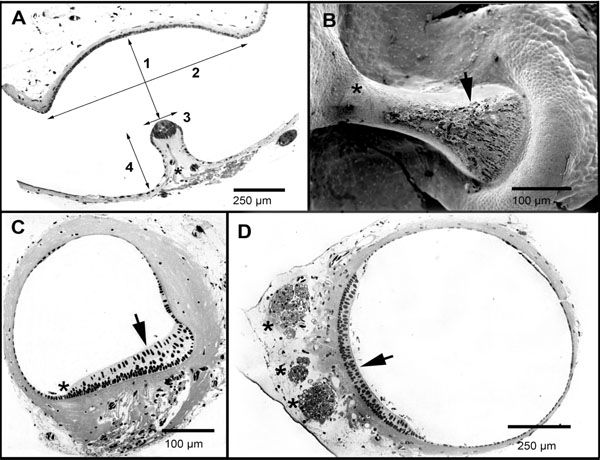 ). Morphological measurements obtained from the three ampullae are shown in Table 1. The lateral canal ampulla turned out to be the largest, with a volume 1.68 times bigger than that of the anterior canal and 1.18 times bigger than that of the posterior canal. This larger volume was mainly due to the fact that the lateral canal ampulla had a bigger cupular space, its cupula is 1.24 and 1.34 times higher than that of the posterior and of the anterior canals respectively (Table 1). The utricle opening of the lateral canal ampulla was 2.38 and 1.62 times that of the posterior and anterior canals respectively.
). Morphological measurements obtained from the three ampullae are shown in Table 1. The lateral canal ampulla turned out to be the largest, with a volume 1.68 times bigger than that of the anterior canal and 1.18 times bigger than that of the posterior canal. This larger volume was mainly due to the fact that the lateral canal ampulla had a bigger cupular space, its cupula is 1.24 and 1.34 times higher than that of the posterior and of the anterior canals respectively (Table 1). The utricle opening of the lateral canal ampulla was 2.38 and 1.62 times that of the posterior and anterior canals respectively.
The anterior and posterior SC cristae were both symmetric, showing a central enlargement. They had about 450 hair cells each. The lateral canal crista was found to be non-symmetric, increasing in its cross section towards the external side of the SC (Fig. 3B ,C
,C ). It showed no central enlargement and had about 550 hair cells [28Cruz-Vera R. Patrón de inervación, ultraestructura y biofísica de los canales semicirculares en el axolotl (Ambystoma mexicanum) In: Tesis de Licencitura Escuela de Ciencias Quìmicas. México: Universidad Autónoma de Puebla 1994.]. It is worth noting that the lateral canal crista is 3.33 times thicker than the anterior and the posterior canal cristae (Tables 1 and 2); this probably means a completely different cupular elasticity.
). It showed no central enlargement and had about 550 hair cells [28Cruz-Vera R. Patrón de inervación, ultraestructura y biofísica de los canales semicirculares en el axolotl (Ambystoma mexicanum) In: Tesis de Licencitura Escuela de Ciencias Quìmicas. México: Universidad Autónoma de Puebla 1994.]. It is worth noting that the lateral canal crista is 3.33 times thicker than the anterior and the posterior canal cristae (Tables 1 and 2); this probably means a completely different cupular elasticity.
Differences in the position of the ampullary crista are worth noting. While those of the posterior and the anterior canals are positioned on the outer arch of the ampulla wall, with the cupula extending from the crista across the ampulla to the inner arch, that of the lateral canal is positioned on the inner arch of the circuit, with the cupula extending to the outer arch. By the use of the scanning electron microscopy, we have searched for evidences of the attachment of the cupula to the lateral walls of the ampulla. No conclusive evidence for a cupular attachment to the lateral wall of the ampulla, nor direct evidence for the existence of a cleft was found (Fig. 3B ).
).
The utricle is a cylindrical organ with a quasi-circular transverse section (Fig. 3D ). The utricle length (l) is 3.16 ± 0.13 mm (n = 9) and its maximum diameter is 0.79 ± 0.11 mm (n = 7). The sensorial macula is positioned in the ventral side of the utricle. The contribution of the utricle to the SC circuits is variable. The utricle contribution to the SC circuits (distinguished in Table 1 as utricle fraction) varies for the three SCs. The utricle forms 32% of the anterior SC circuit, 47.2% of the lateral canal, and 32% of the posterior canal. It is not clear to which extent the endolymph mass in the utricle influences the overall response of the system; however, our results imply that the effective endolymph mass in the lateral canal is probably larger than that found in the posterior and anterior canals. In the axolotl, anterior and lateral SC opening in the ampullary side of the duct forms a ridge dividing the utricle in two halves. This suggests that there may be significant mutual effects between these two canals.
). The utricle length (l) is 3.16 ± 0.13 mm (n = 9) and its maximum diameter is 0.79 ± 0.11 mm (n = 7). The sensorial macula is positioned in the ventral side of the utricle. The contribution of the utricle to the SC circuits is variable. The utricle contribution to the SC circuits (distinguished in Table 1 as utricle fraction) varies for the three SCs. The utricle forms 32% of the anterior SC circuit, 47.2% of the lateral canal, and 32% of the posterior canal. It is not clear to which extent the endolymph mass in the utricle influences the overall response of the system; however, our results imply that the effective endolymph mass in the lateral canal is probably larger than that found in the posterior and anterior canals. In the axolotl, anterior and lateral SC opening in the ampullary side of the duct forms a ridge dividing the utricle in two halves. This suggests that there may be significant mutual effects between these two canals.
4.2. . Simplified Mathematical Model with Morphological Parameters
The mathematical method summarized in section 2.3 can be expanded to account for a more realistic form of semicircular canals including various sections with different radius (e.g., utriculus, ampulla). For example, when a0 (ampulla region II) ≥ a1 (SC duct, region I), and region III corresponding to the utricle with length L > 0:
In this case, an enlargement of the SC is introduced, where
According to the statistical data given in Table 1, it can be considered as if there was a cleft in the posterior canal (ampulla height - (cupula height + crista height)) = 0.02 mm that is why a0 - b = 0.01 mm. Using the data from Tables 1 and 2 (δ = 0.006 mm, a0 = 0.34 mm, L = 2.8 mm and k = 2.2) we have the inequality
In this case in which the cupula was modeled as a piston, the existence of a cleft between the cupula and the ampulla walls originates an additional dissipative force, which is equal to:
this expression is negligible; therefore, the model presented in equation (27 b) can be simplified
This equation (27c) shows that it is irrelevant whether there is a cleft in the cupula or not. If we assume that viscosity of the endolymph is similar to that reported in mans: ν = 0.8 mm2/sec [29Shipov AA, Kondrachuk AV, Sirenko SP. Biomehanika vestibuliarnogo Apparata Ed Slovo Moscow 1997. (in Russian)]. Since viscosity of endolymph depends on temperature, it is very probable that endolymph of the axolotl inner ear could be bigger. Then we obtain for the small time constant:
This result is in agreement with analogous calculations obtained previously [7Van Buskirk WC. The effect of the utricle on fluid flow in the semicircular canals Ann Biomed Eng 1977; 5: 1-11.].
Let us consider the oscillations of the membrane in response to the periodic stimulus V=d cos σt. According to equation (14), the displacement of the membrane in the absolute coordinate system
and the boundary conditions
It can be shown that for ao<< 1 the equality
where
The results of the theoretical and numerical analysis of the cupula-membrane reaction in response to a periodic stimulus are presented in Fig. (4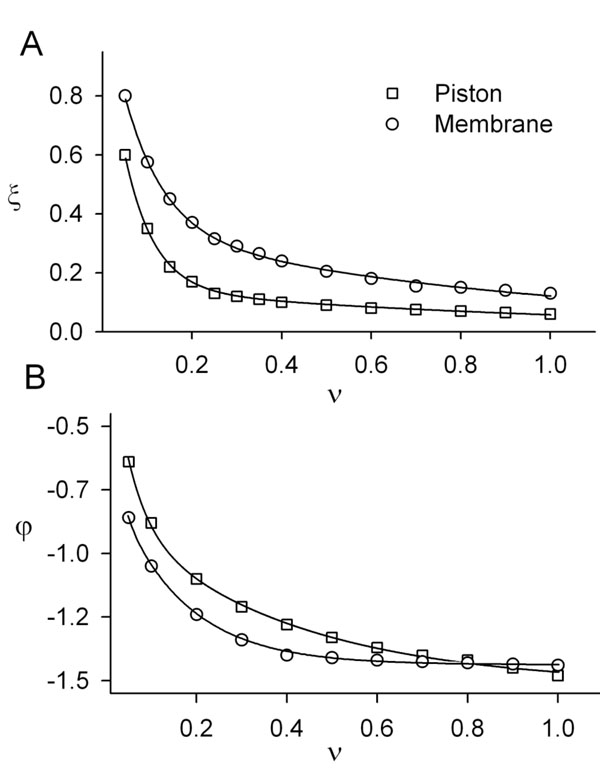 ). For comparison, curves of the amplitude and phase as a function of the frequency of the cupula-piston model are also shown.
). For comparison, curves of the amplitude and phase as a function of the frequency of the cupula-piston model are also shown.
Based on these results, it can be concluded that for periodic stimuli of low frequency a simplified model of the type shown in equation (27) can be used.
4.3. Simplified Mathematical Model for Three Channels System
By using the cinematic model of the mutual effects of SCs [29Shipov AA, Kondrachuk AV, Sirenko SP. Biomehanika vestibuliarnogo Apparata Ed Slovo Moscow 1997. (in Russian)] an approximate model of finite dimension for the cupula-endolymphatic system ampullary wall for the three SCs can be developed:
where λi is the mutual effect coefficient between SCs, a1i is the respective SC duct radius. Due to the fact that the anterior and posterior SCs have a part in common, the flow of endolymph in each of this canals influences the response of the other one. It has also been shown that lateral canal endolymph flow may influence both anterior and posterior canal response [30Petukhov SV. Mathematical modelling of the physics of the semicircular canal in man Functioning of the vestibular system under oscillatory movement of the head Cosmic Biol Problems 1975; 31: 14-64. (in Russian)]. Since in the axolotl there seems to be also a common segment in the anterior and lateral canals, then the endolymph flow in one of these canals will influence the response of the other. As a consequence of the fact that five (their total number is nine) of the interaction coefficients are not equal to zero, we have
λ12 ≠ 0, λ13 ≠ 0, λ21 ≠ 0, λ23 ≠ 0, λ31 ≠ 0, and λ11 = λ22 = λ33 = λ32 = 0 (canals numbered as: anterior 1, posterior 2, and lateral 3). In addition, the product λ13λ23 < 0 and λ12 > 0, λ21 > 0 [15Astakhova TG. Mathematical model of the semicircular canal of the vestibular system as an angular acceleration sensor Moscow Univ Mech Bull 1989; ser.1(No 1): 69-72. (in Russian), 29Shipov AA, Kondrachuk AV, Sirenko SP. Biomehanika vestibuliarnogo Apparata Ed Slovo Moscow 1997. (in Russian)].
Morphological parameters (Table 1) can be used to calculate anatomical parameters of the model (Table 2). A mathematical model (27) with morphological parameters for the dynamics of the SCs can be expressed as follows:
(32)
The coefficients which appear in mathematical model (32) were derived from the mean values given in Table 1. In this model (32) it is worth noting that there are different parameters to characterize the elasticity of the cupula (γi) which is a consequence of the differences in the morphology of the SC crista among the three canals.
In this way, we have five parameters related to the semicircular canal relations of mutual influence λ12 , λ21, λ12, λ21, λ13, λ23, λ31, and four unknown parameters one for the endolymph viscocity ν and three for the elasticity (γ1, γ2, γ3,one for each canal). For the identification of these parameters it is necessary to perform some dynamical experiments. The number of experiments needed must be determined based on the confidence intervals corresponding to the mean quadratic deviations given in Table 1.
5. DISCUSION
To evaluate the complexity of sensory coding in the vestibular endorgans and vestibular system modelling we need to consider the cupula-endolymph model here presented (equation 27c) in the context of the sensory processes shown in Fig. (1 ). supposing that the dynamics of the receptor potential and of the spike encoder may be adequately modeled by Hodgkin and Huxley type ordinary non-linear differential equations of fourth order, and if it is proposed that other processes represented in Fig. (1
). supposing that the dynamics of the receptor potential and of the spike encoder may be adequately modeled by Hodgkin and Huxley type ordinary non-linear differential equations of fourth order, and if it is proposed that other processes represented in Fig. (1 ) are of order one, then a simplified model of the vestibular endorgan will be of 12th order [5]. By assuming that the main requirement for this model is the strict dependence of its parameters upon physiological processes, it will be shown that a detailed analysis which considers some aspects of the activation and inactivation of various ionic currents, or a detailed cupula-endolymp model, will imply the experimental identification of 40 to 50 parameters. This is the reason why development of simplified models of the cupula-endolymph system, that may give an approximated operation of the system without the need to include so many parameters or increase the modelling complexity, is desired.
) are of order one, then a simplified model of the vestibular endorgan will be of 12th order [5]. By assuming that the main requirement for this model is the strict dependence of its parameters upon physiological processes, it will be shown that a detailed analysis which considers some aspects of the activation and inactivation of various ionic currents, or a detailed cupula-endolymp model, will imply the experimental identification of 40 to 50 parameters. This is the reason why development of simplified models of the cupula-endolymph system, that may give an approximated operation of the system without the need to include so many parameters or increase the modelling complexity, is desired.
Nowdays, the study and mathematical modelling of the cupula-endolymph system is similar, in a certain way, to the study of the gyroscope in the years 1930 to 1950: in the beginning an approximate theory of the gyroscope precession was used to account for the behavior of this mechanical device. Later, very detailed models of the mutational oscillation were developed. In the late 50s with the aid of Tikhonov's mathematical method there was a rigorous reduction of the very complex mutational equations to approximated precession equations [24Novozhilov IV. Fractional analysis methods of motion decomposition. Berlin: Birkhäuser 1997.]. Analogously, the very complex and precise differential equations system proposed for the cupula-endolymph system [11Rabbit RD, Damiano ER. A hydroelastic model of macromechanics in the endolymphatic vestibular canal J Fluid Mech 1992; 238: 337-69., 12Rabbitt RD. Directional coding of the dimensional movements by the vestibular semicircular canals Biol Cybern 1999; 80: 417-31., 22Damiano ER, Rabbit RD. A singular perturbation model of fluid dynamics in the vestibular semicircular canal and ampula J Fluid Mech 1996; 307: 333-72.] can be converted into an approximated model by using Galerkin`s mathematical method.
The main advantage of the model here presented is that the coefficients of the model are known functions of morphological and dynamical parameters of the SCs. Thus, based on the morphological measurements of the SCs, it is possible to incorporate the data directly into the model. Our model (27) is a Steinhausen like model in which all model coefficients are functions of physiological parameters, then data derived from physiological experiments and morphological measurements allow to correct the model coefficients thus improving the description of the cupula-endolymph mechanical coupling. In addition, model (27) is simpler than those expressed with differential equations with partial derivatives, or integer-differential equations [11Rabbit RD, Damiano ER. A hydroelastic model of macromechanics in the endolymphatic vestibular canal J Fluid Mech 1992; 238: 337-69.,12Rabbitt RD. Directional coding of the dimensional movements by the vestibular semicircular canals Biol Cybern 1999; 80: 417-31.,17Damiano ER. A poroelastic continuum model of the cupula partition and the response dynamics of the vestibular semicircular canal J Biomech Eng 1999; 131: 449-60.,22Damiano ER, Rabbit RD. A singular perturbation model of fluid dynamics in the vestibular semicircular canal and ampula J Fluid Mech 1996; 307: 333-72.]. Moreover, detailed models are equivalent to simplified one for a restricted range of frequencies coinciding with the expected range of function for the vertebrate vestibular endorgans [23].
The presence of the coefficient of expansion k for human SCs is of about 5 and for the axolotl, it is about 2. From the dynamic equation (27b) we obtain the static equation:
thus the coefficient of expansion k and the presence of utricle longitude l act as an amplifier of the displacement of the cupula. Therefore, a study of dynamical consequences of the specific morphology of SC can be performed. The presence of the utricle in our model leads to an increase of the incoming signal as can be deduced from equation (27). The utricle contribution to the lateral and anterior canal circuits is larger than that related to the posterior canal (32). Also, the influence of the geometry of the canal (elliptical or circular) could be considered in the mathematical model, in our case we used a toroidal form (with mean radius, Table 1) for the SCs.
Modelling the cupula as a piston allows for important simplifications. It is a mathematical abstraction in which no consideration is given to the piston attachment. The system acquires the equilibrium position of the cupula when static fluid pressure exists. Since endolymph flow is laminar, the velocity is nearly nil close to the wall of the canal, whereas the central part of the cupula will be subjected to greater deformation, performing a diaphragm- or piston-like motion. Thus it is probable that even having a lateral cleft, no macroscopic flow of endolymph through the cupula will take place. Therefore, experiments using dyes directed to demonstrate that there is a cleft in the cupula could not be sufficient to define this point [31Hillman DE, McLaren JW. Displacement configuration of semicircular canal cupulae Neuroscience 1979; 4: 1989-2000.]. The exact morphology of the cupula is still under discussion, and there is evidence suggesting that a cleft (septum cruciatum) exists in the posterior SC of some animals [32Hunter-Duvar IM. An electron microscopic study of the vestibular sensory epithelium Acta Otolaryngol 1983; 95: 494-507.]. Light -microscopic observations of the cupula in-vivo have also shown that the base of the cupula is at the level of the tips of the cilia [33Nagel G, Neugebauer DC, Schmidt B, Thurm U. Structures transmitting stimulatory force to the sensory hairs of vestibular ampullae of fishes and frog Cell Tissue Res 1991; 265: 567-78.]. By analogy with the saccule, it is very likely that the subcupular space is filled by a columnar filament layer bridged by the hair bundles of sensory cells [21Kachar B, Parakkal M, Fex J. Structural basis for mechanical transduction in the frog vestibular sensory apparatus: I. The otolithic membrane Hear Res 1990; 45: 179-90.].
In relation to a possible endolymph leak in the cleft between the piston and the ampulla wall, a theoretical mechanical model in the form here presented shows negligible effects of this phenomenon on the dynamics of the cupula-endolymph system. The inclusion of the lubrication hydrodynamic layer between the cupula-piston and ampulla wall introduces an additional viscous damping in equation (27). It is also shown that according to our assumptions the viscous damping can be ignored. On the basis of the inequality
it can be concluded that the viscosity forces which may appear in the cleft between the cupula and the wall of the SC are small if compared with viscosity forces caused by the movement of the endolymph in the SC. We conclude that the existence of an endolymph flow through the cupula has no relevant consequence for the mathematical modelling of cupular displacement.
The physiological significance of morphological asymmetries in the crista ampullaris between the lateral canal and the anterior and the posterior canals has not been addressed. Undoubtedly, the structure of the crista ampullaris and the cupula may play a significant role in determining the cupular displacement, although there are evidences suggesting that the elastic element has a minor role in determining the mechanical behaviour of the semicircular duct system [18Muller M, Verhagen JH. Optimization of the mechanical performance of a two-duct semicircular duct system- part 2 excitation of endolymph movements J Theor Biol 2002; 216(4): 425-.]. The model here presented (32) also implies the consideration of a more complex configuration including the other two SC and a coefficient of mutual influence between them [29Shipov AA, Kondrachuk AV, Sirenko SP. Biomehanika vestibuliarnogo Apparata Ed Slovo Moscow 1997. (in Russian)].
The morphological data here presented allows for the identification of the anatomical parameters of the model. In general our data are in agreement with previous descriptions of amphibian inner ear, and constitute, to our best knowledge, the first ultrastructural quantification of SCs and utricular morphology of the axolotl. The relationship between the circuit radius (R), and the SC duct radius (r) was Ra = 6.2 ra, RL = 8.7 rL and Rp = 5.8 rp. These size relations suggest that compared with other vertebrates the axolotl SCs have low sensitivity and high frequency of response [18Muller M, Verhagen JH. Optimization of the mechanical performance of a two-duct semicircular duct system- part 2 excitation of endolymph movements J Theor Biol 2002; 216(4): 425-.].
Model parameters were classified in two groups: anatomical and dynamical. The progress in parameter identification will be based on the planning of dynamical experiments. Unknown parameters such as cinematic viscosity of the endolymph, elasticity coefficient of the cupula and effective viscosity may be approximated by analysis of the mathematical model of the cupula-endolymph system. For the identification of these parameters two pathways are possible: i) direct measurement of the cupula displacement in dynamical experiments and then, by means of identification algorithms, to estimate the unknown parameters. ii) to register the output of the system (activity of SC afferent neurons) in dynamical experiments. In this case, the addition of various compartments to the model are surely needed to account for the processes that will take place at the hair cell, the synapse and the primary afferent neuron level, and the use of parameter estimation is also needed.
CONCLUSION
Despite the existence of previous models of the vestibular system the inclusion of non physiological variables makes of them less usable for prediction and interpretation of the model output. Our proposal of a simplified model of the cupula-endolymph coupling mechanism eases the interpretation of results and set up the bases to more appropriate transfer functions to be used in future prosthesis for the vestibule or to control position-dependent mechanisms. Some of the predictions of the model are presented altogether with detailed anatomical data of the vestibule in the axolotl. The future use of this model using morphological parameters from different animals, including humans, and including additional compartments describing transduction function, hair cell response, synapse and dynamics of the afferent neurons may allow to generate a more complete view of vestibular system operation, contributing to the development of technical devices for inertial navigation.
ACKNOWLEDGEMENTS
The authors wish to thank Gertrudis Payas for proof reading of the manuscript. This research was partially supported by UC-MEXUS-CONACyT grant from the University of California at Riverside (grant CN-07-111), and CONACyT grant 46511 to E.S.